Jump Consistent Hash Algorithm

In this article we discuss the Jump Consistent Hash algorithm, a minimalist and efficient consistent hashing algorithm.

Hashing and Consistent Hashing

A hash function, or hash function, maps the elements of a large definition field into a small finite value field. The elements in the value domain are sometimes called buckets, and the size of the value domain is also referred to as the number of buckets.

MD5 is a common hash function that maps data of any size (the larger definition field) into a 16-byte hash (the smaller finite value field). The simplest hash function is modulo, which maps all integers (the larger definition field) into an integer interval (the smaller finite value field).

Suppose our server has 3 worker processes, serving the user at the same time. These worker processes have the same function and store the user’s state data. So how to decide which worker process serves a user? The easiest way to do this is to take the user ID and assign it to one of the 3 processes.

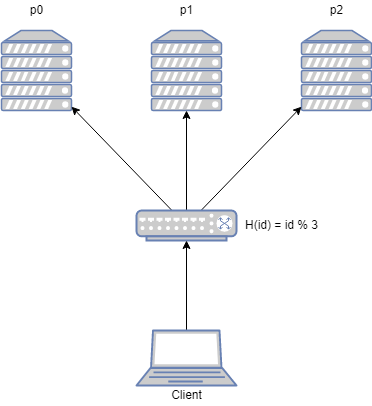
This seems to be working perfectly. As the number of users grows, 3 worker processes are overstretched and the server needs to be scaled up. We need to add one more worker process and have 4 worker processes serving the users at the same time. This is where the problem arises.

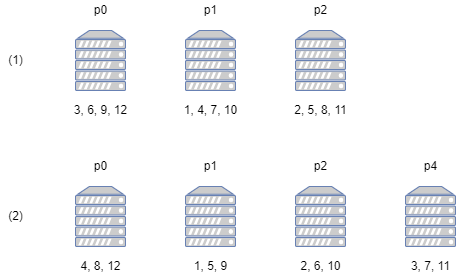
Suppose that before the expansion the server has 12 users online with IDs 1 to 12, then they are distributed among 3 processes as shown in figure (1) above. Now we add a worker process, which requires the users to be distributed among 4 processes, and the hash function should be changed to remainder of 4, which will cause the distribution of clients to change to the case shown in figure (2) above. As mentioned earlier, the server processes store the state data of the users; this expansion will cause the processes of almost all users to change, which will necessitate a large number of data migration operations. If the server has a large number of users online, the cost of the scaling operation becomes unacceptable.

To solve this problem, consistent hash has been proposed. Consistent hash is a special class of hash functions, which is characterized by the fact that when the number of buckets increases from $N-1$ to $N$, only $\frac{1}{N}$ of the mapping results change on average. Looking at the above example, we only need to take one user from each of p0, p1 and p2 to migrate to p4 when expanding the capacity, which means that only $\frac{12}{4} = 3$ IDs are changed.

There are various consistent hashing algorithms. The earliest consistent hashing algorithm was proposed by Karger et al. It associates buckets in a clockwise ring, which is used in the Chord algorithm. In this paper, we present the Jump Consistent Hash algorithm proposed by John Lamping et al. in 2014. It is extremely simple, with only 7 lines of code

1
2
3
4
5
6
7
8
9

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
    int64_t b = ­1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}

At first glance, you may be confused: 2862933555777941757ULL What is it? What is left-right shift to floating point and then divide? Is it really possible to change the mapping of $\frac{1}{N}$ in just a few lines? Let’s explore this amazing algorithm step by step.

Probability-based hashing algorithm

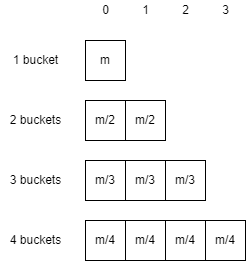
As mentioned before, when the number of buckets increases from $N-1$ to $N$, the mapping result of $\frac{1}{N}$ changes. In other words, if the hash function maps $m$ elements to bucket 1, all elements are mapped to bucket 0, i.e., the hash value is 0. If the number of buckets becomes 2, then $\frac{m}{2}$ elements are moved from bucket 0 to bucket 1, i.e., the hash value becomes 1. When the number of buckets becomes 4, then $\frac{m}{4}$ elements are moved from the first three buckets to bucket 3, and so on.

Consider the problem from another perspective: Suppose there is an element that maps to bucket 0 when there are 1 buckets. When the number of buckets becomes 2, it has $\frac{1}{2}$ when the probability moves to bucket 1; when the number of buckets becomes 3, it has $\frac{1}{3}$ when the probability moves to bucket 2, and so on. That is, no matter which bucket the element is currently in, it has a probability of moving to bucket $N-1$ whenever the number of buckets changes from $N-1$ to $N$. Thus, we transform this problem into a probability problem.

Based on this idea, we can implement a consistent hashing algorithm. Since the algorithm is based on random probability, in order to make each hash result consistent, we make random seeds of the values of the elements.

1
2
3
4
5
6
7
8
9

int consistent_hash(int key, int num_buckets) {
    srand(key);
    int b = 0;
    for (int n = 2; n <= num_buckets; ++n) {
        if ((double)rand() / RAND_MAX < 1.0 / n)
            b = n - 1;
    }
    return b;
}

This algorithm simulates the case where the number of buckets grows. When the number of buckets is 1, the element must be in bucket 0, so there is an initial b = 0. Each time the number of buckets increases to n, the element has a probability of moving to bucket n - 1, which is the newly added bucket.

Improved algorithm

This algorithm can achieve consistent hashing, but it is a bit slow, with a time complexity of $\mathrm{O}(n)$. Is there a faster way? We note that when buckets are added, there is only a small probability that the elements will move to the newly added buckets, and a large probability that they will stay in place. If we could compute only when the elements move, the algorithm would be much faster.

Notice that elements only move as buckets are added, and each move is necessarily to the newest bucket. That is, if an element moves to bucket $b$, the bucket must have increased to $b+1$ to cause the move. Suppose an element just moved to bucket $b$ when the bucket grew to $b + 1$, can we find the target of the next move of this element?

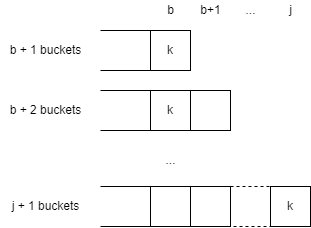
Suppose the target of the next move of the element is bucket $j$, meaning that the element does not move until the bucket is increased by $j + 1$, in other words, the element does not move until the bucket is increased by $b+2, b+3, \cdots, j$. If we find the maximum $j$ such that the element does not move when the bucket increases to $b+2, b+3, \cdots, j$, then we have found the target $j$ for the next move.

In terms of probability, the probability that the next move of an element is at least $j$ is equal to the probability that the bucket is increased to $b+2, b+3, \cdots, j$ without a move. We know that the probability of an element moving when the bucket increases to $N$ is $\frac{1}{N}$, so the probability of not moving is $\frac{N-1}{N}$. Thus we have:

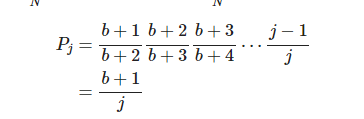
Now let’s reverse the idea. Now that the element moves to $b$ when the bucket is increased to $b+1$, we need to determine where this element will move next $j$. We can generate a random number $r$ between 0 and 1, such that $P_j = r$. Then we can determine $j$:

The improved algorithm is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

int consistent_hash(int key, int num_buckets) {
    srand(key);
    int b = ­1, j = 0;
    while (j < num_buckets) {
        b = j;
        r = (double)rand() / RAND_MAX;
        j = floor((b + 1) / r);
    }
    return b;
}

In the above algorithm, each iteration finds the next position j of the element by using the formula (1), until j >= num_buckets.

Linear congruence generator

To further improve the algorithm, we can use our own implementation of the random function, rather than relying on the system. Here we use the Linear congruential generator. This is an old random number generation algorithm, which is easy to implement. Its random numbers are generated iteratively, and the iterative formula is as follows:

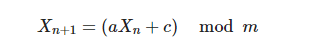
$a, c, m$ are constants. $m$ is a positive integer, called modulus; $a$ is called multiplier, $0 \lt a \lt m$; $c$ is called increment, $0 \le c \lt m$. Each iteration of the algorithm generates a new random number $X_{n+1}$ based on an old random number $X_n$. The initial value of the iteration $X_0$ is called the seed, $0 \le X_0 \lt m$.

In the Jump consistent hash algorithm, each iteration is like this:

1
2

key = key * 2862933555777941757ULL + 1;
j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));

The randomized algorithm has a multiplier of 2862933555777941757, an increment of 1, and a modulus of 0x100000000000000000000. There is no need to take the modulus manually, just let the integer overflow naturally. So each iteration generates a random number in the range 0 to 0xffffffffffffff. Here (key >> 33) + 1 takes the high 31 bits of the random number and adds one more, from 1 to 0x80000000. Then we divide 0x80000000 by it to get the inverse of the probability. The final multiplication by b + 1 is the position of the next move of the element j.

Summary

So there’s a lot of wisdom in a little code. There are a few things that this article hasn’t gone into, such as the rigorous proof of the probability formula; why the multiplier is 2862933555777941757, and why the increment is 1. The random number generation algorithm is a very important topic, and this paper can only go so far. Compared to Karger’s algorithm, the Jump Consistent Hash algorithm is simple, fast, and does not require additional memory. Of course, it has a disadvantage: its value domain can only be the set of non-negative integers less than N. This means that it is not possible to simply remove the intermediate numbers. This means that you cannot simply remove the middle bucket, which would result in a discontinuity in the value domain.