The background of memory authentication computing is trusted computing, for example, to do some processing involving important data, from the software, we hope that even if the system is illegally accessed by the attacker, we can ensure that important information will not be leaked; from the hardware, we hope that even if the system can be attacked by some physical operations (such as exporting or modifying memory, etc.), we can ensure that the attacker cannot read or tamper with the data.
The following is mainly based on Hardware Mechanisms for Memory Authentication: A Survey of Existing Techniques and Engines, a 2009 article.
Threat Model
As a defense mechanism, it is important to first determine the capabilities of the attacker. A common threat model assumes that an attacker has physical control and can manipulate data in memory at will, but cannot read or modify data inside the CPU. That is, only the data inside the CPU chip is trusted; anything outside the chip is within the attacker’s control. A simple idea is to make the data stored in the memory encrypted, so how can an attacker attack the encrypted data? Here are a few typical attack methods.
- Spoofing attack: Changing in-memory data to arbitrary attacker-controlled data; this attack can be solved by signatures
- Splicing or relocation attack: Move a section of memory data to another section, so that the signature of the data is still correct; so the address needs to be taken into account when calculating the signature, so that the address has changed, the verification of the signature will fail.
- Replay attack: If the memory of the same address has changed, the attacker can write the old memory data in again, so that the signature and address are correct; to prevent replay attacks, you also need to introduce counters or random nonce
Authentication Primitives
In order to defend against the above-mentioned attacks, the following ideas are mentioned in the article mentioned above.
One is Hash Function, which divides the memory into many blocks and calculates a cryptographic Hash for each block to be stored in the chip, then when reading data, the whole block of data is read in and the Hash is calculated once and compared with the result stored in the chip; when writing data, the Hash of the modified data is calculated again and updated to the storage in the chip. The disadvantages of this method are that there is no encryption, the attacker can see the content, but once modified, it will be discovered by the CPU (unless there is a Hash conflict), and the storage cost is high: for example, for a 512-bit block, each block calculates a 128-bit Hash, which wastes 25% of the space, and the on-chip space is very valuable.
Second, the MAC Function, which is the message authentication code of cryptography, requires a Key that is saved in the slice; since the attacker does not know the password, according to the nature of the MAC, the attacker cannot tamper with the data or forge the MAC, so the computed MAC can be directly saved into memory as well. In order to defend against replay attacks, we need to introduce random nonce and save the nonce in the slice, for example, for every 512-bit data, 64-bit nonce is saved, so 12.5% of the space in the slice needs to be saved, which is still quite a lot. The MAC itself is not encrypted, so if you do not want the attacker to see the plaintext, you also need to encrypt it.
The third is Block-Level AREA, which means that the plaintext and random nonce are stitched together and saved in memory using a block encryption algorithm; when decrypting, the final nonce is verified to be the same as the one saved in the slice. This method is similar to MAC, which does the encryption thing and also needs to save the random nonce corresponding to each block of data in the chip.
Integrity Tree
For example, if we want to protect 1GB of memory, then we need to keep hundreds of MB of data inside the chip, which is too large for on-chip storage. In this case, we can use Merkle Tree or similar methods commonly used in blockchain to trade time for space.
The main idea of this method is to first divide the memory into many blocks, which correspond to the leaf nodes of a tree; build a tree from the bottom up, and each node can verify the integrity of its child nodes, then after log(n) layers of the tree, only a small root node will be obtained in the end, and only the root node needs to be kept in the slice.
To verify the integrity of a particular block, start from the leaf node corresponding to this block, keep computing a value and compare it with the father node; then recursively go up and finally compute the value of the root node and compare it with the value saved in the slice. The complexity of verification in this way is O(log), but the data saved in the slice becomes O(1), so it is time for space. When updating the data, it is similarly calculated step by step from the leaf node and finally updates the value of the root node.
The space wasted by this method, considering all the data saved by non-leaf nodes, is half the total size of the data if it is a binary tree, but the advantage is that most of it can be saved in memory, so it is relatively easy to implement. The disadvantage is that each read and write requires O(logn) number of memory accesses and calculations, and the overhead is relatively high.
The above mentioned method of calculating the value of the parent node is a Merkle Tree if it uses the cryptographic Hash function; its authentication process is read-only and can be parallelized, but the update process is serial because the Hash is calculated step by step from the child nodes, and the parent node depends on the Hash result of the child nodes.
Another design is Parallelizable Authentication Tree (PAT), which uses MAC instead of Hash, each node keeps a random nonce and the computed MAC value, the MAC input at the bottom layer is the actual data, the MAC input at the other layers is the nonce of the child nodes, and finally the nonce value of the last MAC used is kept within the slice The nonce value of the last MAC used is stored in the slice. The advantage of this is that when updating, each layer can be counted in parallel, because the MAC input is the nonce value and does not involve the MAC calculation results of the child nodes. The disadvantage is that more data, i.e. MAC and nonce, have to be kept.
Another design is the Tamper-Evident Counter Tree (TEC-Tree), which computes the Block-level AREA mentioned above. similarly, the bottom layer is encrypted with data and random nonce, while the other layers are encrypted with random nonce of the child nodes, and then stitched with the nonce of this layer. When verifying, the bottom layer is decrypted first, then the data is judged to match, then the upper layer is decrypted again, and the nonce is judged to match, recursively, and finally the nonce of the root is decrypted and matched with the nonce saved in the slice. When updating, we can similarly produce a series of nonce at once, and then encrypt the result of each layer in parallel.
Finally, to quote a comparison from the article.

It can be seen that the latter two algorithms can update the nodes of the tree in parallel and also need to save more data.
Cached Trees
From the Integrity Tree algorithm above, we can see that each read or write has to access memory O(logn) times, which has a huge impact on performance. A simple idea is to save some frequently accessed tree nodes in the in-chip cache, so as to reduce the number of memory accesses; furthermore, if it is believed that the attacker cannot tamper with the in-chip cache, then it is straightforward to assume that the in-chip nodes are all trusted, and when verifying and updating, it is only necessary to traverse from the leaf nodes to the in-chip cache nodes.
The Bonsai Merkle Tree
To further reduce space consumption, the Bonsai Merkle Tree (MKT) is based on the idea that instead of encrypting each memory block, the MAC is computed once for C consecutive memory blocks, and an additional counter is added, where the input to the MAC computation is the data, address, and counter. So similarly, the Merkle Tree protects these counters, and since the number of counter bits is smaller, the space overhead can be further reduced, and the number of tree layers is also smaller.
Specifically, to avoid replay attacks, each time the data is updated, the counter is added by one, similar to the original use of a sufficiently long (e.g., 64-bit) random nonce. However, the counter has a limited number of bits, and if the overflow is bypassed, it gives the attacker a chance to perform a replay attack, so the key has to be changed once and re-encrypted.
Re-encryption is very time-consuming, so a two-level counter is designed: a 7-bit local counter, which adds one to each update, and a 64-bit global counter, which adds one when one of the local counters overflows. This is equivalent to making a common prefix of counter, so that when the memory access is more even, for example, each local counter takes turns to add one, then only a small range of memory needs to be re-encrypted each time, reducing This reduces the overhead.
Some related algorithms are mentioned later in the article, so I won’t continue to summarize them here.
Mountable Merkle Tree
Let’s take a look at the Mountable Merkle Tree design mentioned in Scalable Memory Protection in the Penglai Enclave. It mainly considers dynamically variable protected memory regions, such as the mentioned microservices scenario, and the access to the protected memory region is time-local, so it is thought that instead of constructing a Merkle Tree corresponding to the complete memory, it allows some subtrees to not exist. Specifically, it designs a concept of Sub-root nodes, which corresponds to the middle layer of the Merkle Tree. This layer up is pre-allocated and mostly kept in memory, with the root nodes kept within the slice, and this layer down is dynamically allocated. For example, if an application creates a new enclave, it needs a new protected memory area, and then dynamically allocates several Merkle Trees to the Sub-root nodes layer, which become new subtrees.
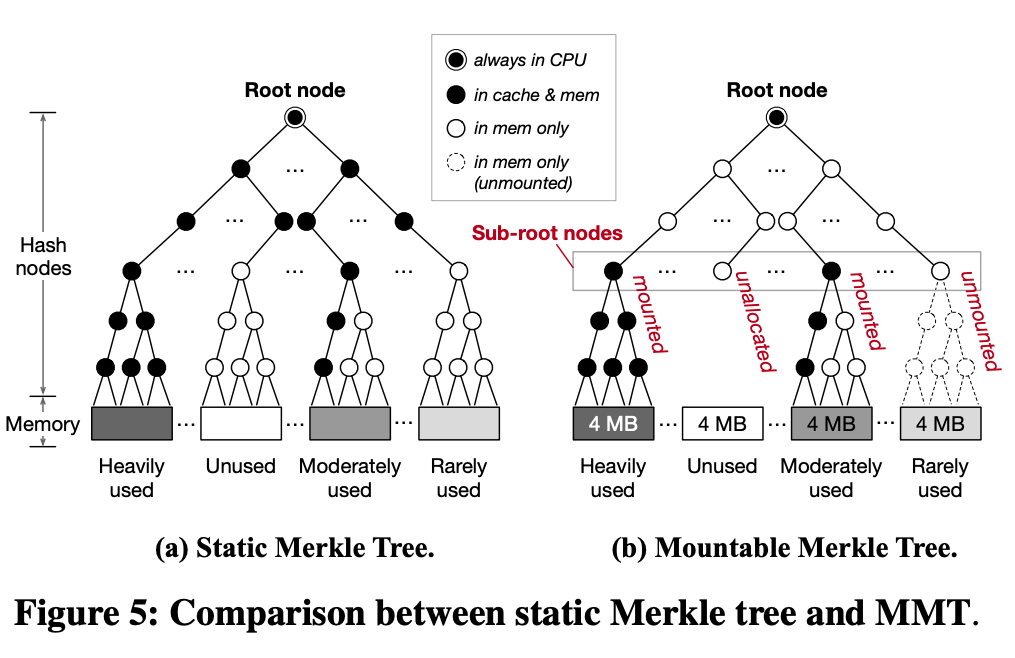
Since the space inside the slice is limited, a caching approach is adopted here to keep only a part of the commonly used tree nodes inside the slice; if a subtree has not been accessed, it can be swapped out into memory. If an existing enclave is deleted, then the corresponding subtree can be deleted to reduce the memory space occupation.