Dynamic Password Algorith

Dynamic password, also known as One Time Password (OTP), is an efficient, simple and relatively secure password generation algorithm, which can be found everywhere in our lives and work, and as developers, we have more or less integrated two-step authentication mechanism in our business systems. So, what is the principle of dynamic password algorithm?

Pre-reading guide

• With this article, you can learn about the following.
  • Background knowledge of dynamic passwords
  • Classification of dynamic passwords
  • Different dynamic password generation algorithms, HOTP and TOTP
  • A simple Ruby programming language implementation of HOTP and TOTP
  • Notes on each of the two types of algorithms
• For the sake of space, I will not discuss the following points, but if you are interested, you can refer to the references given at the end of my article for.
  • An analysis of the security of different dynamic passwords
  • How to ensure that the password is not used twice during the validity period of a timed dynamic password

Background on dynamic passwords

From my point of view, a dynamic password is a password that is regenerated with the occurrence of a certain event (password being used, passage of a certain amount of time, etc.), because the biggest advantage of dynamic passwords themselves is that they are resistant to repeated execution attacks (replay attack), which can well avoid the defects of similar static passwords that can be brute-force cracked, etc. In reality, they are generally used The combination of “static password + dynamic password” two-factor authentication, we also call two-step authentication.

The dynamic password actually appeared in our lives a long time ago, before the development of mobile payments, Internet banking was the most popular online payment channel, when banks to ensure that everyone’s Internet banking account payment security, will be issued to Internet banking customers with a dynamic password card, such as the Bank of China electronic password card (according to the time difference in the generation of new passwords, password card comes with a battery to ensure continuous use for several years), or ICBC’s electronic banking password card (Internet banking payment web page generates a different row serial number each time, the user scratches the coating on the password card according to the specified row combination to obtain the password, the password expires after use), or the mandatory requirement of the bank SMS verification code, these can be included in the category of dynamic password.

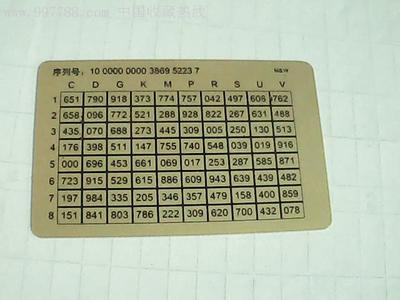
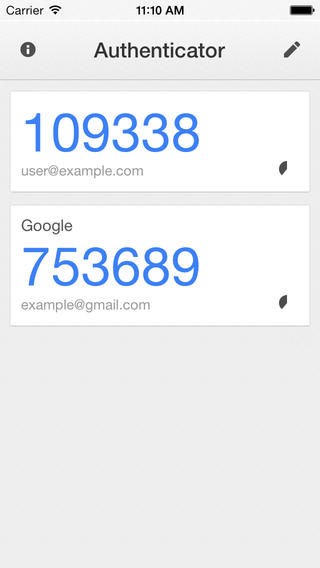
And with the development of the mobile Internet and the continuous improvement of the intelligence of mobile devices, the synchronization ability between devices has increased significantly, and the dynamic password generation technology that used to rely on independent devices soon evolved into dynamic password generation software on cell phones to generate dynamic passwords in the form of cell phone software has greatly improved the portability of dynamic passwords, and a user a cell phone can manage any number of dynamic passwords generation, which also makes the promotion of two-step verification on the site much less resistance, because in the past customers may refuse to open the two-step verification mechanism because it is too cumbersome to use the password card, thus exposing their accounts to risk. The most well-known dynamic password generation software is Google’s Authenticator APP.

A journey of dynamic cryptographic algorithm exploration

Classification of dynamic passwords

In general, there are two types of common dynamic passwords.

• Counted-use: After the output of the counted-use OTP, it can be used at any time until the next successful use, when the counter is added 1 to generate a new password. The algorithm used to achieve the counted use of dynamic passwords is called HOTP, which will be introduced next.
• Timed use: Timed use of OTP can set the password validity time, ranging from 30 seconds to two minutes, and the OTP is discarded after the authentication, the next authentication must use a new password. The algorithm used to implement the time-based dynamic password is called TOTP, which will be introduced next.

Before the real algorithm is introduced, it is necessary to add that the basic authentication principle of dynamic passwords is to share the key, also known as the seed key, and the same seed key used for an event count, or time value of the cryptographic algorithm calculation, the use of algorithms such as symmetric algorithms, HASH, HMAC. Remember this, this is the basis for the implementation of all dynamic cryptographic algorithms.

HOTP

HOTP algorithm, full name is “An HMAC-Based One-Time Password Algorithm”, is a one-time password generation algorithm based on event counting, detailed algorithm description can be found in RFC 4226. In fact, the algorithm itself is very simple, and the algorithm itself can be described by two short expressions.

1

HOTP(K,C) = Truncate(HMAC-SHA-1(K,C)) PWD(K,C,digit) = HOTP(K,C) mod 10^Digit

In the above equation.

• K represents the key we share between the authentication server side and the password generation side (client device), in RFC 4226, the authors require the minimum length of the shared key to be 128 bits, while the authors themselves recommend using a 160-bit length key
• C is the value of the event count, an 8-byte integer called the moving factor, and it should be noted that the integer value of C needs to be expressed as a binary string, e.g., if the event count is 3, C is "11" (the leading binary digit 0 is omitted here)
• HMAC-SHA-1 means to encrypt the shared key and the shift factor with the SHA1 algorithm of HMAC, and get the encryption result of 160 bits length (20 bytes)
• Truncate is the truncation function, which will be described later.
• digit specifies the length of the dynamic password, for example, we commonly use a 6-bit dynamic password

Truncate truncate function

Since the SHA-1 algorithm is an existing algorithm and not the focus of our discussion, the Truncate function is the most critical part of the entire algorithm. The following is a step-by-step description of the Truncate function.

1
2
3

DT(String) // String = String[0]…String[19] Let OffsetBits be the low-order 4 bits of
String[19] Offset = StToNum(OffsetBits) // 0 <= OffSet <= 15 Let P = String[OffSet]…
String[OffSet+3] Return the Last 31 bits of P

Combined with the above formula, it is roughly described as follows.

1. first select the 4 bits of the last byte of the low byte bit from the result of the 20-byte length obtained by SHA-1 algorithm encryption in the first step (note: the big-endian storage used in the dynamic cipher algorithm).
2. convert the binary value of these 4 bits to an unscented integer value to obtain a number between 0 and 15 (inclusive), which is used as the offset from 0 in the 20 bytes.
3. then intercept 4 consecutive bytes (32 bits) starting from the specified offset, and finally return the next 31 bits of the 32 bits.

Returning to the algorithm itself, after obtaining the 31-bit truncated result, we convert it to an integer value with no punctuation at the big end, which takes values from 0 to 2^31, i.e., 0 to 2.147483648E9, and finally we modulo this number by multiplying by 10 (digit exponent range 1-10) to obtain a remainder value, which is preceded by 0 to obtain the specified number of bits of We get the string with the specified number of digits.

Code Example

The following code example is also available at Gist.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

require 'openssl'

def hotp(secret, counter, digits = 6)
  hash = OpenSSL::HMAC.digest(OpenSSL::Digest.new('sha1'), secret, int_to_bytestring(counter))  # SHA-1 算法加密
  "%0#{digits}i" % (truncate(hash) % 10**digits)  # 取模获取指定长度数字密码
end

def truncate(string)
  offset = string.bytes.last & 0xf           # 取最后一个字节
  partial = string.bytes[offset..offset+3]   # 从偏移量开始，连续取 4 个字节
  partial.pack("C*").unpack("N").first & 0x7fffffff    # 取后面 31 位结果后得到整数
end

def int_to_bytestring(int, padding = 8)
  result = []
  until int == 0
    result << (int & 0xFF).chr
    int >>= 8
  end
  result.reverse.join.rjust(padding, 0.chr)
end

The above algorithm implements a small amount of code, the core is just a number of mask operations and bit manipulation according to the algorithm description.

Password Failure Mechanism

From the above analysis, we can see that the generation of a dynamic password depends on the shared key and the value of the move factor, which remains constant, and ultimately only the move factor determines the result of the password generation. Therefore, in the HOTP algorithm, it is required that each time a password is successfully verified, the authentication server side as well as the password generator (client side) should add 1 to the counter value to ensure that a new password is obtained.

However, a problem is introduced here, if the communication between the authentication server and the password generator is out of sync due to a communication failure or other unforeseen circumstances, then the passwords generated by the two sides will not match correctly. In order to solve this problem, the algorithm suggests in the analysis that the authentication server side can take the initiative to try whether the new password regenerated after the counter minus 1 is the same as the password submitted by the client after the password verification fails, and if so, it can be assumed that the client counter is not synchronized, in which case it can pass the verification and ask the client to resynchronize the counter value.

In addition to the above mentioned problem of the counter not being synchronized, I was thinking that if the client has multiple password generators (assuming iPad and iPhone) generating passwords for the same account, then the synchronization of the counter between multiple devices may require a separate consideration.

Summary

The algorithm for HOTP is actually much more concise than I thought before reading the algorithm, and still robust enough. The algorithm itself cleverly uses a cryptographic algorithm to encrypt the shared key and counter to ensure that the two dynamic password generation factors are not tampered with, and then a truncate function to obtain a random decimal integer of up to 10 bits, ultimately enabling support for dynamic passwords of 1 - 10 bits in length. The simplicity of the algorithm itself ensures that the algorithm itself can be implemented on a variety of devices.

TOTP

The TOTP algorithm, known as TOTP: Time-Based One-Time Password Algorithm, is based on the HOTP algorithm and is centered on changing the move factor from event counting in HOTP to time difference. The complete description of the TOTP algorithm can be found in RFC 6238, and its formula description is very simple.

1

TOTP = HOTP(K, T) // T is an integer and represents the number of time steps between the initial counter time T0 and the current Unix time More specifically, T = (Current Unix time - T0) / X, where the default floor function is used in the computation.

Generally speaking, the time difference used in TOTP is the current timestamp, and TOTP divides the time difference by the time window (password validity, default 30 seconds) to get the time window count, which is used as the shift factor of the dynamic password algorithm, so that it is easy to get a time-based dynamic password based on the HOTP algorithm.

Note: RFC 6238 mentions that in the TOTP algorithm, a different keyed hash algorithm can be specified, for example, in HOTP the HMAC-SHA1 algorithm is used, while in TOTP, in addition, HMAC-SHA256 or HMAC-SHA512 can be used.

1

TOTP implementations MAY use HMAC-SHA-256 or HMAC-SHA-512 functions, based on SHA-256 or SHA-512 [SHA2] hash functions, instead of the HMAC-SHA-1 function that has been specified for the HOTP computation in [RFC4226].

Code Example

The following code example is also available at Gist.

1
2
3
4
5
6
7

require 'hotp'

def totp(secret, digits = 6, step = 30, initial_time = 0)
  steps = (Time.now.to_i - initial_time) / step

  hotp(secret, steps, digits)
end

See, extremely short implementation code! A time-counting dynamic password algorithm was born. Such a simple algorithm, but the cornerstone of the security operation of many business systems, quite a four-two-thousand pounds of pleasure!

Questions to discuss

1. the main problem in the ROTP algorithm is the synchronization of counters, and TOTP is no exception, but the problem lies in the synchronization of time between the server and the client, due to the development of the Internet now, coupled with mobile devices are generally set in accordance with the network time device time, basically the relative synchronization of time is not a problem.
2. another problem of time synchronization is actually a boundary problem, if the client generates the password for exactly 29 seconds, and due to network delays and other reasons, the server accepts the verification just at the first second of the next time window, this time will lead to password verification failure. Therefore, TOTP algorithm in its algorithm discussion also suggests that the server can try to regenerate the password after the failed password verification by subtracting 1 from its own time window value, and if the verification passes, it means that the failed verification is caused by the boundary problem of the time window, and then the password verification can be considered as passed.
3. Another advantage of time-based dynamic password is that it avoids the counter synchronization problem among multiple devices based on counters, because each device as well as the server can calibrate itself with the network time (common time standard) without relying on the server’s time.

Google Authenticator

In Google Authenticator’s open source project the README explicitly mentions.

These implementations support the HMAC-Based One-time Password (HOTP) algorithm specified in RFC 4226 and the Time-based One-time Password (TOTP) algorithm specified in RFC 6238.

At this point, we also understand that the core of the Google Authenticator algorithm is also HOTP and TOTP, after understanding the core of the entire dynamic password algorithm, there is a feeling of clarity?

Summary

This article briefly introduced two common types of dynamic password generation algorithms, the algorithm itself is simple and uncomplicated, efficient and robust enough. The purpose of this article is to facilitate people like me who want to understand the core of the algorithm. There is still a lot of discussion about the security aspects of the algorithms themselves in the RFC documentation, so check it out if you are interested.