Today we talk about an important computer concept that you may have heard of, but rarely delve into, and that is byte order (Endianness).
1. Concepts
Byte order refers to the order in which multiple bytes of data are arranged in memory . This is rather abstract, but it is well understood using a graphical explanation.
Memory is like a row of rooms, and each byte is a room. Each room has a door number (memory address), starting from 0, then 1, 2 ……

The address of byte 0 is small and is called low memory; the address of byte 3 is large and is called high memory.
Now there is a value abcd to be put into these rooms, one number in each room, so there are two ways to put it.
The first way is to put the first a in the low address (number 0) and the last d in the high address (number 3).
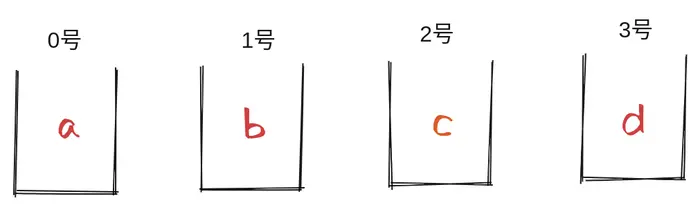
This arrangement is called " big-endian" (BE), i.e., the big head comes first, because a is the big head (the most important number) of abcd.
The second way is that the first a is placed at the high address (address 3) and the last d is placed at the low address (address 0).
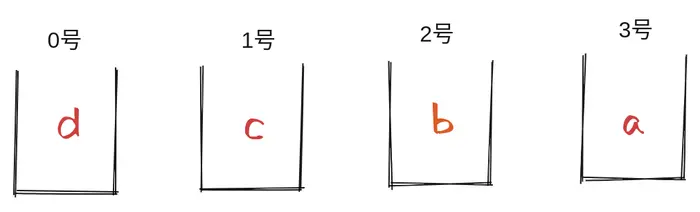
This arrangement is called " little-endian" (LE for short), which means that the small head d comes first.
The big-end order and the little-end order are collectively called the byte order, and the two names come from the 18th century English novel “Gulliver’s Travels”. A country was divided into two factions: one believed that eggs should be eaten from the big end, called the “big end”; the other believed that eggs should be eaten from the small end, called the “small end”. The two factions were unable to convince each other, and eventually even went to war over it.

2. Readability
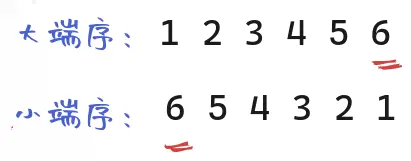
For human beings, readability is different for different byte sequences. The reading habit of most countries is to read from left to right.
The highest bit of the big end sequence is on the left and the lowest bit is on the right, in line with reading habits. Therefore, for people in these countries, the left-to-right big end sequence is better readable.
But in reality, the right-to-left small end order is less readable but more widely used. x86 and ARM are both CPU architectures that use small end order.
Or to ask another question, why do two different byte orders co-exist, and wouldn’t it be more convenient to unify and specify only one?
The reason is that they have their own applicable scenarios, some scenarios have advantages of large end order, some scenarios have advantages of small end order, the following is an analysis of each one.
3. Checking Parity
Probably the most obvious advantage of the small end order is checking parity, i.e., determining whether a number is odd or even by looking at the digits.
In the case of 123456, for example, the big end sequence is from left to right, and the computer must read all the way to the last digit of the digit 6 to determine that it is an even number.
The small end sequence is right-to-left, and the digit is in the first place. So, if you read the first digit, you can be sure that it is even.
4. Check positive and negative signs
A similar scenario is to check the plus and minus signs to determine whether a number is positive or negative.
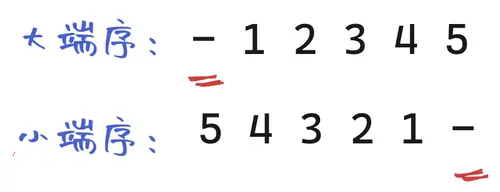
The sign bit of the big terminal sequence is in the first place on the left, and the sign bit of the small terminal sequence is in the last place on the right. Therefore, the large terminal sequence has the advantage that you can tell if it is a negative number by looking at the first bit only.
5. Compare Size
The next operation is to compare the size. Now there are three numbers that need to be compared in size: 43662576, 594, and 2.

The diagram above shows the big end order arrangement, because it is arranged from left to right, so the three numbers are aligned at the right digit. When comparing the sizes, the computer has to read all the bits of each number up to the single digit and then compare them.
If you change to small-end order, it is the following arrangement.

The smallest end order is right-to-left, so the three digits are aligned in the first place. The computer then does not need to read all the bits, and whichever number is read first without the next bit is the smallest. For example, the number 2 does not have a second bit, so when it reads the second bit, it knows it is the smallest.
So, when comparing sizes, the small end order has an advantage.
6. Multiplication
Next, look at the multiplication operation again.
Multiplication is a place-by-place multiplication, with each round of multiplication going forward.
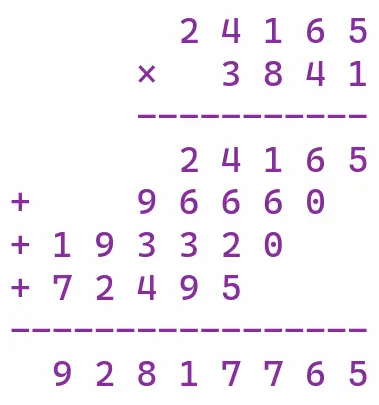
The above figure shows 24165 multiplied by 3841 in big terminal order. big terminal order multiplication is left-rounded, i.e., it expands to the left, and you must wait until the results of each round are available (four rounds in the above example), then add them up and write them to memory uniformly.
If we change to small terminal multiplication, we do not need to wait for the result of the next round, and each round can be written directly to memory.

The above figure shows the multiplication of 24165 by 3841 in the small end sequence, which is an expansion to the right, with the left boundary unchanged. Once the result of each round is written to memory, there is no need to move it, and any changes later on only require changing the corresponding bit.
Therefore, multiplication in the small-end sequence has a clear advantage.
7. Arbitrary precision integers
The computation-from-lower-bit feature of the previous example is particularly useful for arbitrary-precision integers. Arbitrary precision integers, also known as big integers, can hold integers of any size.
It is implemented internally by dividing the integer into smaller units, usually uint32 (unsigned 32-bit integer) or uint64 (unsigned 64-bit integer), and combining them together in order.
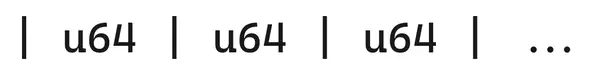
In the case of a large terminal sequence, the first u64 is the largest part of this integer. Once this number changes and needs to be rounded, all subsequent bits must be shifted and rewritten. When rounding occurs in the small end order, often all bits do not need to be shifted.
Another advantage of the small end order is that if the byte-by-byte operation starts with a single digit (such as multiplication and addition), you can operate one u64 at a time from left to right, and read the next one after the previous one. This is not possible in big-endian order, where the entire number must be read before the operation is performed.
8. Changing the type
As a final example, C has a cast operation that forces a change in the data type of a variable, such as forcing a 32-bit integer to a 16-bit integer.

In the above figure, the 32-bit integer 0x00000001 is changed to 16-bit integer 0x0001, and the big terminal sequence is truncated by two bytes, so the pointer to this address must be moved backward by two bytes.
The small end sequence does not have this problem, the truncation is the next two bytes, the first address is unchanged, so the pointer does not need to move.
9. Summary
In summary, the advantages of large and small end sequences are as follows.
If bit-by-bit arithmetic is required, or if the arithmetic needs to start from a single digit, the small end order has the advantage. Conversely, if the operation involves only high bits, or if the readability of the data is more important, the big end order is dominant.
10. Reference Links
- On Endianness, Karl Stenerud