Golang: Explaining container/heap

The heap container is provided in golang’s container package. What can this container be used for and how does it do it? This article explains the heap, the heap package, the uses of the heap package, and the implementation of the heap package, starting from the source code of golang 1.9.3.

1 What is heap

Let’s start by explaining what a heap (Heap) is.

According to Wikipedia

Heap (Heap) is a generic term for a special class of data structures in computer science. A heap is usually an array of objects that can be thought of as a tree. In a queue, the scheduler repeatedly fetches the first job in the queue and runs it, because in reality some tasks with short time will wait for a long time to finish, or some jobs that are not short, but have importance, should have the same priority. The heap is a data structure designed to solve such problems.

Logical definition: A sequence of n elements {k1, k2… ki…kn}, is called a heap when and only when the following relations are satisfied.

`1`	`(ki <= k2i, ki <= k2i+1) or (ki >= k2i, ki >= k2i+1), (i = 1, 2, 3, 4... n/2)`

A heap has the following properties.

Any node is smaller (or larger) than all its descendants, and the smallest element (or the largest element) is at the root of the heap (heap orderliness).
A heap is always a complete tree. That is, the nodes at all levels are filled with elements except the bottom level, and the bottom level is filled from left to right as much as possible.

The difference between a complete binary tree and a full binary tree is shown below.

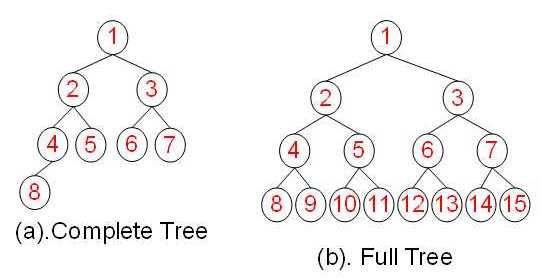
The difference between a complete binary tree and a full binary tree

The heap with the largest root node is called the largest heap or the large root heap, and the heap with the smallest root node is called the smallest heap or the small root heap.

Since heaps are complete binary trees, they can be represented as sequential arrays as follows.

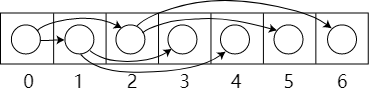
heaps are complete binary trees

Remember these two diagrams, they will be used later.

2 Methods provided by container/heap

After understanding what a heap is, let’s take a look at the container/heap package.

The heap package provides heap methods for types that implement heap.Interface: Init/Push/Pop/Remove/Fix. container/heap is a minimum-valued heap, i.e., the value of each node is less than the value of all elements of its subtree (A heap is a tree with the property that each node is the minimum-valued node in its subtree).

type Interface interface {
    sort.Interface
    Push(x interface{}) // add x as element Len()
    Pop() interface{}   // remove and return element Len() - 1.
}

Since heap.Interface contains sort.Interface, the target type needs to contain the following methods: Len/Less/Swap, Push/Pop.

3 What container/heap can be used for

The container/heap package can be used to construct a priority queue.

Take the priority queue of go src as an example.

Define the PriorityQueue type.

// An Item is something we manage in a priority queue.
type Item struct {
    value    string // The value of the item; arbitrary.
    priority int    // The priority of the item in the queue.
    // The index is needed by update and is maintained by the heap.Interface methods.
    index int // The index of the item in the heap.
}

// A PriorityQueue implements heap.Interface and holds Items.
type PriorityQueue []*Item

func (pq PriorityQueue) Len() int { return len(pq) }

func (pq PriorityQueue) Less(i, j int) bool {
    // We want Pop to give us the highest, not lowest, priority so we use greater than here.
    return pq[i].priority > pq[j].priority
}

func (pq PriorityQueue) Swap(i, j int) {
    pq[i], pq[j] = pq[j], pq[i]
    pq[i].index = i
    pq[j].index = j
}

func (pq *PriorityQueue) Push(x interface{}) {
    n := len(*pq)
    item := x.(*Item)
    item.index = n
    *pq = append(*pq, item)
}

func (pq *PriorityQueue) Pop() interface{} {
    old := *pq
    n := len(old)
    item := old[n-1]
    item.index = -1 // for safety
    *pq = old[0 : n-1]
    return item
}

// update modifies the priority and value of an Item in the queue.
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
    item.value = value
    item.priority = priority
    heap.Fix(pq, item.index)
}

PriorityQueue is essentially an *Item array, whose Len/Less/Swap are more common arrays used to sort the functions that need to be defined, while Push, Pop are methods that use arrays to insert,. PriorityQueue also provides the update method. Note that since you usually want the priority queue to pop out the highest priority elements, the Less method is written in reverse.

After defining the above methods, PriorityQueue is ready to use the container/heap package.

In the following code, a pq array is defined from the items map, the length is the size of the hash, and heap.Init is called to initialize the pq array; after that, an element with priority 1 is added to the queue and the queue is updated; finally, the elements are popped from the queue accordingly, and it can be seen that the elements are sorted according to the priority when they are popped.

// This example creates a PriorityQueue with some items, adds and manipulates an item,
// and then removes the items in priority order.
func Example_priorityQueue() {
    // Some items and their priorities.
    items := map[string]int{
        "banana": 3, "apple": 2, "pear": 4,
    }

    // Create a priority queue, put the items in it, and
    // establish the priority queue (heap) invariants.
    pq := make(PriorityQueue, len(items))
    i := 0
    for value, priority := range items {
        pq[i] = &Item{
            value:    value,
            priority: priority,
            index:    i,
        }
        i++
    }
    heap.Init(&pq)

    // Insert a new item and then modify its priority.
    item := &Item{
        value:    "orange",
        priority: 1,
    }
    heap.Push(&pq, item)
    pq.update(item, item.value, 5)

    // Take the items out; they arrive in decreasing priority order.
    for pq.Len() > 0 {
        item := heap.Pop(&pq).(*Item)
        fmt.Printf("%.2d:%s ", item.priority, item.value)
    }
    // Output:
    // 05:orange 04:pear 03:banana 02:apple
}

4 How heap is done

The example given above is amazing to say the least. How does container/heap do it?

4.1 heap.Init

Let’s first look at the heap.Init function.

// A heap must be initialized before any of the heap operations
// can be used. Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// Its complexity is O(n) where n = h.Len().
//
func Init(h Interface) {
    // heapify
    n := h.Len()
    for i := n/2 - 1; i >= 0; i-- {
        down(h, i, n)
    }
}

The key point is the down function.

func down(h Interface, i0, n int) bool {
    i := i0
    for {
        j1 := 2*i + 1
        if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
            break
        }
        j := j1 // left child
        if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
            j = j2 // = 2*i + 2  // right child
        }
        if !h.Less(j, i) {
            break
        }
        h.Swap(i, j)
        i = j
    }
    return i > i0
}

The function of the down function is very simple: given the type, the index of the element in the array that needs to be sunk, the length of the heap, the element is sunk to the appropriate position in the subtree corresponding to that element, thus satisfying the requirement that the subtree be the smallest heap.

Remember the previous diagram of the sequential array representation of the heap? Combine this with the implementation of the down function: pick any element i, compare it with its children 2i+1 and 2i+2, and if element i is smaller than its children, swap element i with the smaller of the two children (j), thus ensuring that the requirement of the smallest tree is satisfied (first down); child j may also have its children, continue comparing and swapping until the end of the array or element i is smaller than both of its children, jumping out of the loop.

Why is it that element i, which is smaller than both of its children, can jump out of the loop and not continue? This is because, in the Init function, the first element to start down (sink) is the n/2 - 1th one, and it is guaranteed to always start down from the last subtree (as in the previous figure, n=8 or n=9, n/2-1 is always 4), so it is guaranteed that when Init->down, if element i is smaller than both of its children, then the subtree corresponding to that element, is the minimum heap.

Init, after traversal, guarantees that the array to be Init is a minimal heap.

4.2 heap.Push

Let’s see again how heap.Push guarantees that the sequential array remains a minimal heap when new elements are inserted.

// Push pushes the element x onto the heap. The complexity is
// O(log(n)) where n = h.Len().
func Push(h Interface, x interface{}) {
    h.Push(x)
    up(h, h.Len()-1)
}

First call h.Push to push the elements into the user-defined type, the aforementioned PriorityQueue. The array append, there is nothing to say. Since the element is inserted at the end of the array, the up function needs to be called to “float” it.

Let’s see how up floats.

func up(h Interface, j int) {
    for {
        i := (j - 1) / 2 // parent
        if i == j || !h.Less(j, i) {
            break
        }
        h.Swap(i, j)
        j = i
    }
}

If element j is smaller than parent i, the two nodes are swapped and the comparison continues to the next higher parent until the root node, or element j, is larger than parent i.

In this way, it is ensured that the sequential array in which the new elements are inserted remains a minimal heap after up.

4.3 heap.Pop

// Pop removes the minimum element (according to Less) from the heap
// and returns it. The complexity is O(log(n)) where n = h.Len().
// It is equivalent to Remove(h, 0).
func Pop(h Interface) interface{} {
    n := h.Len() - 1
    h.Swap(0, n)
    down(h, 0, n)
    return h.Pop()
}

The previous Pop function of PriorityQueue actually takes the :n-1 sub-array of the sequential array, so the purpose of heap.Pop is to swap the root node (0) with the element of the last node, and sink the element of the new root node to the right position to satisfy the requirement of the minimum heap; finally, call the Pop function of PriorityQueue again to get the last element.

4.4 heap.Fix

The update function of PriorityQueue actually relies on heap.Fix when modifying the priority of the elements.

// Fix re-establishes the heap ordering after the element at index i has changed its value.
// Changing the value of the element at index i and then calling Fix is equivalent to,
// but less expensive than, calling Remove(h, i) followed by a Push of the new value.
// The complexity is O(log(n)) where n = h.Len().
func Fix(h Interface, i int) {
    if !down(h, i, h.Len()) {
        up(h, i)
    }
}

The code is relatively clear: if it can sink, it sinks, otherwise it floats. the return value of down can express whether there has been a sink (i.e. whether there has been a swap).

4.5 heap.Remove

The Remove function is not used in the priority queue example, so let’s look at the code directly.

// Remove removes the element at index i from the heap.
// The complexity is O(log(n)) where n = h.Len().
//
func Remove(h Interface, i int) interface{} {
    n := h.Len() - 1
    if n != i {
        h.Swap(i, n)
        if !down(h, i, n) {
            up(h, i)
        }
    }
    return h.Pop()
}

First swap the node i to be deleted with the last node n, and then sink or float the new node i to the appropriate position. This piece of logic is similar to Fix, but note that you cannot call heap.Fix directly, the last element is to be deleted and cannot participate in Fix.

Table of Contents