Serialize Roaring Bitmap to JSON

Recently, a bitmap index was used in the implementation of a data structure, and this article will talk about the bitmap in a rough way.

I. What is a bitmap?

Bitmap indexing is implemented using a bit array (also called a bitset, often referred to as a bitmap, the name bitmap is used hereafter). A bitmap is a mapping from a domain (usually a range of integers) to the values in the set {0, 1}.

`1`	`Mapping: f(x) -> {0, 1}, x is an element in the set of [0, n).`

Take the set {1, 2, 5} with n = 8 as an example.

f(0) = 0
f(1) = 1
f(2) = 1
f(3) = 0
f(4) = 0
f(5) = 1
f(6) = 0
f(7) = 0

If we use bit to represent the value obtained after mapping, we will get a binary number 0b00100110 (the value on the rightmost bit indicates the existence of the value 0 in the set), so that we can use a byte-sized value 0b00100110 to represent the existence of the values at each position in the set {1, 2, 5}.

We see that compared to using a byte array to represent the set {1, 2, 5} (even with 8 values, it would take at least 8x8 = 64 bytes), bitmap definitely has a higher space utilization. Also, with the &, |, ^, etc. operations of bitmap, we can easily and efficiently obtain the results of set intersection, merge, Top-K, and other set operations.

However, traditional bitmaps do not always bring space savings. For example, if we want to represent a set like {1, 2, 10, 50000000}, then using a traditional bitmap will bring a large space overhead. For such a set with sparse elements, the traditional bitmap implementation loses its advantage, and a compressed bitmap becomes a better choice.

II. Compressed bitmap

Compressed bitmaps can support sparse sets well while retaining the space and high performance advantages of traditional bitmaps for set manipulation. The most common scheme for compressing bitmaps is RLE (run-length encoding), a rough understanding of which is to count consecutive 0s and 1s separately, for example, the following bitmap can be compressed and encoded as n 0s and m and 1s.

`1`	`0b0000....00001111...111`

The RLE scheme (and its variants) has a good compression ratio and is very efficient in coding and decoding. However, its shortcoming is that it is difficult to access a random bit, and each time you access a specific bit, you have to decompress it from scratch. If you want to compute the intersection of two large bitmaps, you have to decompress the whole large bitmap.

A compressed bitmap scheme called roaring bitmap can solve the above problem.

III. Introduction to the working principle of roaring bitmap

The roaring bitmap works like this: it divides the integer number [0, 4294967296) that can be represented by a 32-bit integer into 2^16 chunks (e.g., [0, 2^16), [2^16, 2x2^16), …) . When adding a number to the roaring bitmap or getting the existence of a number from the roaring bitmap, the roaring bitmap determines which trunk the number is in by the first 16 bits of the number. Once the trunk is determined, the container that actually stores the last 16 bits of the number can be found by using the container pointer associated with the trunk and located by a lookup algorithm in the container.

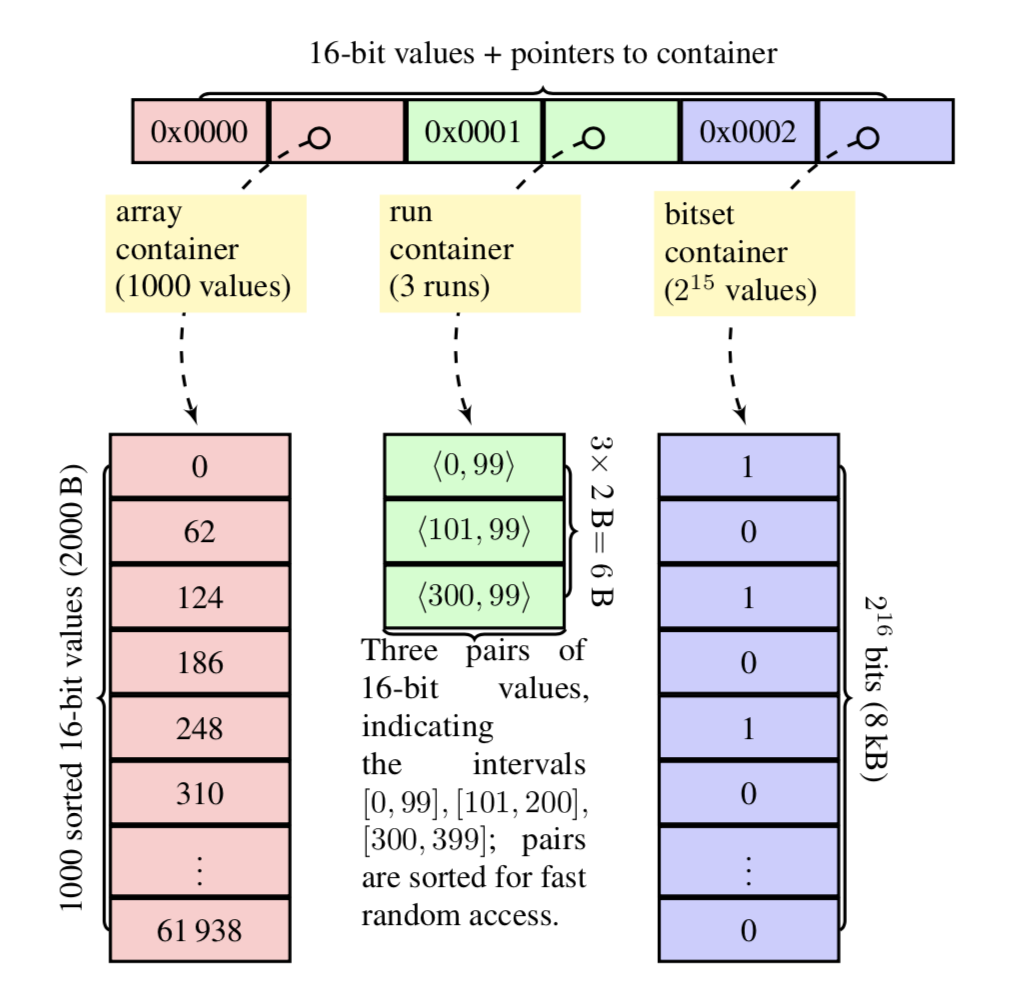
How roaring bitmap works

As shown above: there is more than one type of container associated with the trunk of a roaring bitmap.

array container: This is an ordered 16bit integer array, and the default container type, storing up to 4096 values. When this number is exceeded, storage in a bitset container is considered.
bitset container: this is an uncompressed bitmap with 2^16 bits.
run container: This is a container type that uses RLE compression and is suitable for storing continuous values. As you can also see from the above figure, this container stores a number pair <s,l>, which represents the range of values [s, s + l]

The roaring bitmap selects the appropriate container type based on the characteristics of the numbers in the trunk, and this selection is dynamic, with the goal of minimizing memory usage. When we add or remove values to the roaring bitmap, the container type of the corresponding trunk may change. However, from an overall perspective, the roaring bitmap supports fast random access to a bit regardless of the container type used. Also roaring bitmap is easier to implement at the implementation level to take advantage of the high performance instructions provided by modern cpu and is cache friendly.

IV. The effect of roaring bitmap

The official implementation of roaring bitmap is available in many major languages, among which the Go language implementation is roaring package. roaring package is very simple to use, and the following is a simple example.

package main

import (
    "fmt"

    "github.com/RoaringBitmap/roaring"
)

func main() {
    rb := roaring.NewBitmap()
    rb.Add(1)
    rb.Add(100000000)
    fmt.Println(rb.String())
    fmt.Println(rb.Contains(1))
    fmt.Println(rb.Contains(2))
    fmt.Println(rb.Contains(100000000))

    fmt.Println("cardinality:", rb.GetCardinality())
    fmt.Println("rb size=", rb.GetSizeInBytes())
}

Running the example gives the following results.

{1,100000000}
true
false
true
cardinality: 2
rb size= 16

We see that a sparse set of {1, 100000000} mapped to a roaring bitmap takes up only 16 bytes of space (compared to a non-compressed bitmap).

Here is an example of mapping a collection of random integers up to 3000w to a roaring bitmap.

func main() {
    rb := roaring.NewBitmap()

    for i := 0; i < 30000000; i++ {
        rb.Add(uint32(rand.Int31n(30000000)))
    }

    fmt.Println("cardinality:", rb.GetCardinality())
    fmt.Println("rb size=", rb.GetSizeInBytes())
}

Here are the results of its execution.

1
2

cardinality: 18961805
rb size= 3752860

We see that nearly 1900w numbers are added to the set, and the roaring bitmap takes up a total of 3.6MB of memory space, which is not much different from the uncompressed bitmap.

Here is an example of mapping a continuous set of 3000w numbers to a roaring bitmap.

func main() {
    rb := roaring.NewBitmap()

    for i := 0; i < 30000000; i++ {
        rb.Add(uint32(i))
    }

    fmt.Println("cardinality:", rb.GetCardinality())
    fmt.Println("rb size=", rb.GetSizeInBytes())
}

The result of its execution is as follows.

1
2

cardinality: 30000000
rb size= 21912

Obviously for such a continuous set of numbers, the space efficiency of roaring bitmap is very obvious.

V. Serialization of roaring bitmap

The above is a rough introduction to roaring bitmap, if you are interested in roaring bitmap, you can go to its official site or open source project homepage to do in-depth understanding and learning. But what I want to talk about here is the serialization of roaring bitmap, taking serialization to JSON and deserialization from JSON as an example.

Considering the performance issues, json serialization I chose ByteDance open source sonic project. sonic is a Go open source project, but due to its requirements for the ultimate optimization of JSON parsing, the project currently accounts for less than 30% of Go code, more than 60% are assembly code. sonic provides a function interface compatible with the Go standard library json package. sonic also supports streaming I/O mode, which supports serializing a specific type of object to an io.Writer or deserializing data from an io.Reader to a specific type of object, which is also not supported by the standard library json package. The streaming I/O mode is very useful when encountering very large JSON. ioW.riter and Reader can keep your Go application from instantly allocating large amounts of memory or even being oom killed.

But roaring bitmap does not natively provide functions/methods to serialize (marshal) to JSON (or reverse serialize), so how do we serialize a roaring bitmap to a JSON text?The Go standard library json package provides the Marshaler and Unmarshaler interfaces, where The json package can support serialization and deserialization of any custom type that implements these two interfaces. In this respect, the sonic project remains compatible with the Go standard library json package.

However, the roaring.Bitmap type does not implement the Marshaler and Unmarshaler interfaces, and the serialization and deserialization of roaring.Bitmap needs to be done by ourselves.

Then, the first thing we think of is to customize a new type based on roaring.Bitmap, such as MyRB.

// https://github.com/bigwhite/experiments/blob/master/roaring-bitmap-examples/bitmap_json.go
type MyRB struct {
    RB *roaring.Bitmap
}

Then, we give the implementation of MyRB’s MarshalJSON and UnmarshalJSON methods to satisfy the Marshaler and Unmarshaler interfaces.

// https://github.com/bigwhite/experiments/blob/master/roaring-bitmap-examples/bitmap_json.go
func (rb *MyRB) MarshalJSON() ([]byte, error) {
    s, err := rb.RB.ToBase64()
    if err != nil {
        return nil, err
    }

    r := fmt.Sprintf(`{"rb":"%s"}`, s)
    return []byte(r), nil
}

func (rb *MyRB) UnmarshalJSON(data []byte) error {
    // data => {"rb":"OjAAAAEAAAAAAB4AEAAAAAAAAQACAAMABAAFAAYABwAIAAkACgALAAwADQAOAA8AEAARABIAEwAUABUAFgAXABgAGQAaABsAHAAdAB4A"}

    _, err := rb.RB.FromBase64(string(data[7 : len(data)-2]))
    if err != nil {
        return err
    }

    return nil
}

We use the ToBase64 method provided by roaring.Bitmap to convert the roaring bitmap to a base64 string and then serialize it to JSON; the deserialization is done by decoding the JSON data using FromBase64. Let’s test the interconversion between MyRB type and JSON.

// https://github.com/bigwhite/experiments/blob/master/roaring-bitmap-examples/bitmap_json.go

func main() {
    var myrb = MyRB{
        RB: roaring.NewBitmap(),
    }

    for i := 0; i < 31; i++ {
        myrb.RB.Add(uint32(i))
    }
    fmt.Printf("the cardinality of origin bitmap = %d\n", myrb.RB.GetCardinality())

    buf, err := sonic.Marshal(&myrb)
    if err != nil {
        panic(err)
    }

    fmt.Printf("bitmap2json: %s\n", string(buf))

    var myrb1 = MyRB{
        RB: roaring.NewBitmap(),
    }
    err = sonic.Unmarshal(buf, &myrb1)
    if err != nil {
        panic(err)
    }

    fmt.Printf("after json2bitmap, the cardinality of new bitmap = %d\n", myrb1.RB.GetCardinality())
}

Run the example.

1
2
3

the cardinality of origin bitmap = 31
bitmap2json: {"rb":"OjAAAAEAAAAAAB4AEAAAAAAAAQACAAMABAAFAAYABwAIAAkACgALAAwADQAOAA8AEAARABIAEwAUABUAFgAXABgAGQAaABsAHAAdAB4A"}
after json2bitmap, the cardinality of new bitmap = 31

The output is as expected.

Based on MyRB, which supports serialization, and by the way, let’s look at the benchmark comparison between sonic and the standard library json, we write a simple comparison test case.

// https://github.com/bigwhite/experiments/blob/master/roaring-bitmap-examples/benchmark_test.go

type Foo struct {
    N    int    `json:"num"`
    Name string `json:"name"`
    Addr string `json:"addr"`
    Age  string `json:"age"`
    RB   MyRB   `json:"myrb"`
}

func BenchmarkSonicJsonEncode(b *testing.B) {
    var f = Foo{
        N: 5,
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    for i := 0; i < 3000; i++ {
        f.RB.RB.Add(uint32(i))
    }

    b.ReportAllocs()
    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        _, err := sonic.Marshal(&f)
        if err != nil {
            panic(err)
        }
    }
}

func BenchmarkSonicJsonDecode(b *testing.B) {
    var f = Foo{
        N: 5,
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    for i := 0; i < 3000; i++ {
        f.RB.RB.Add(uint32(i))
    }

    buf, err := sonic.Marshal(&f)
    if err != nil {
        panic(err)
    }
    var f1 = Foo{
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    b.ReportAllocs()
    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        err = sonic.Unmarshal(buf, &f1)
        if err != nil {
            panic(err)
        }
    }
}

func BenchmarkStdJsonEncode(b *testing.B) {
    var f = Foo{
        N: 5,
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    for i := 0; i < 3000; i++ {
        f.RB.RB.Add(uint32(i))
    }

    b.ReportAllocs()
    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        _, err := json.Marshal(&f)
        if err != nil {
            panic(err)
        }
    }
}

func BenchmarkStdJsonDecode(b *testing.B) {
    var f = Foo{
        N: 5,
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    for i := 0; i < 3000; i++ {
        f.RB.RB.Add(uint32(i))
    }

    buf, err := json.Marshal(&f)
    if err != nil {
        panic(err)
    }
    var f1 = Foo{
        RB: MyRB{
            RB: roaring.NewBitmap(),
        },
    }

    b.ReportAllocs()
    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        err = json.Unmarshal(buf, &f1)
        if err != nil {
            panic(err)
        }
    }
}

Execute this benchmark.

$go test -bench .
goos: darwin
goarch: amd64
pkg: demo
... ...
BenchmarkSonicJsonEncode-8         71176         16331 ns/op       49218 B/op         13 allocs/op
BenchmarkSonicJsonDecode-8         85080         13710 ns/op       37236 B/op         11 allocs/op
BenchmarkStdJsonEncode-8           24490         49345 ns/op       47409 B/op         10 allocs/op
BenchmarkStdJsonDecode-8           20083         59593 ns/op       29000 B/op         15 allocs/op
PASS
ok      demo    6.166s

As we can see from this benchmark result, sonic is 3 to 4 times faster than the standard library json package.

The code in this article can be downloaded at here.

VI. Ref

https://tonybai.com/2023/02/01/serialize-roaring-bitmap-to-json/

Table of Contents