With the expansion of system size, there are many distributed applications. For example, to ensure the high availability of Redis in a distributed system, we need to build Redis to slot the data, and when the data stored in MySql database reaches a certain size, we need to split the database. In addition to these typical distributed applications, for example, if we want to develop a distributed job scheduling system, the actual nodes executing the jobs have different configurations (CPU, memory, GPU, etc.) and are also distributed in different regions. How do we ensure that jobs are scheduled to the correct node as much as possible, and that the impact on job scheduling is minimized when a new node is added or a node goes down?

To be clear, the problem described above is how to map data objects to different machines according to certain rules, and the most intuitive way we can think of is a hash function, with the help of which we can know exactly which node the data object needs to be mapped to. But can ordinary hash functions solve the problem of mapping data objects that we encounter in distributed systems?

Simple hash

Let’s take the distributed job scheduling system mentioned above as an example, and associate it with the implementation principle of hashmap in Java, which calculates the hash value by hash function on the keys of job data objects. The simplest hash function is to perform a modulo operation on the total number of job execution nodes through the job data object, and the resulting hash value can be regarded as a “hash bucket”, which is the node to which the job should be scheduled.

This seems to be a simple solution to the data object mapping problem, but if we need to add some new compute nodes to the cluster as the system throughput increases, when we calculate the hash value of the data object again, the base of the modulo operation has changed, which will cause the result of data object mapping to change, that is, the nodes of job scheduling have changed, which For some jobs with special needs for configuration, the impact is huge. Therefore, we need to find ways to make this situation does not occur, the root of this situation is the characteristics of the hash algorithm itself, the direct use of modulo this can not be avoided.

The simplest hashing algorithm calculates the hash value of a keyword by modulo operation, and then maps the keyword into a limited address space to facilitate fast retrieval of the keyword. Because the simple hash algorithm only uses the modulo operation, making it has many shortcomings:

  1. Inefficient update of node addition and deletion: If the number of storage nodes in the whole system changes, the hash function of the hashing algorithm also needs to change. For example, add or delete a node is, the hash function will change to hash(key)%(N±1), this change makes all the keywords mapping address space changes, that is, the entire system of all objects mapping address need to be recalculated, so that the system can not make a normal response to external requests, will lead to the system in a state of paralysis.
  2. poor balance: the system using simple hash algorithm does not consider the difference in performance between different nodes, resulting in poor system balance. If the newly added nodes have more computing power due to the hardware performance improvement, the algorithm cannot effectively exploit the node performance difference to improve the system load.
  3. insufficient monotonicity: when a new node is added to the system, the result of the hash function should be able to ensure that the data objects with previously allocated mapped addresses can be mapped to the original address space. (b) The simple hashing algorithm cannot satisfy monotonicity; once the number of nodes changes, then all data objects mapped addresses will change.

Consistent Hashing

The consistent hashing algorithm corrects the shortcomings of the simple hashing algorithm by ensuring that the system removes or adds a node with as little change as possible to the mapping relationship of existing data objects to the address space, i.e., it tries to satisfy the monotonicity of the hashing algorithm.

  1. Ring Hash Space

    Consistent hashing algorithm maps the key values of all data objects into a 32-bit long address space value, i.e., the value space of 0~2^32-1, which is connected at the beginning and end to form a ring, i.e., a closed circle with the first (0) and the last (2^32-1) connected, as shown below: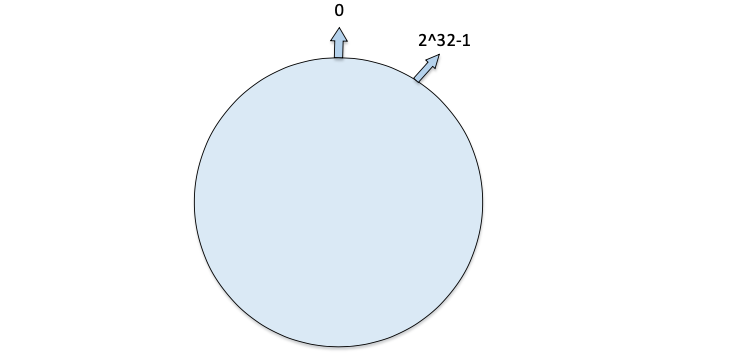

    Ring Hash Space

  2. Map numeric objects to a hash space

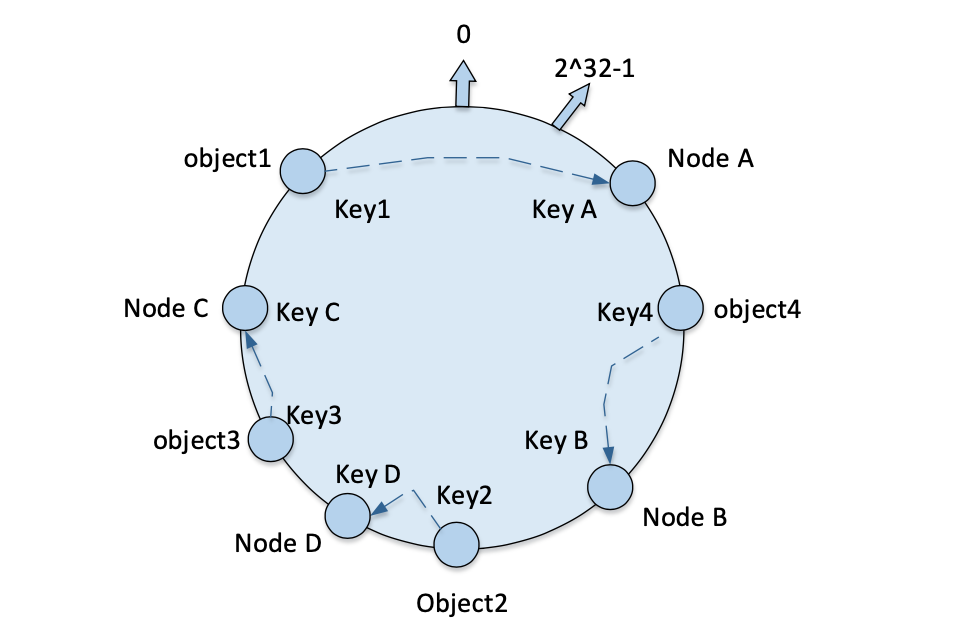
    Map all numeric objects into the ring hash space. Consider such 4 numeric objects: object1~object4, and the hash value calculated by the hash function as the address in the ring address space, so that the 4 numeric objects are distributed on the ring as shown in the figure.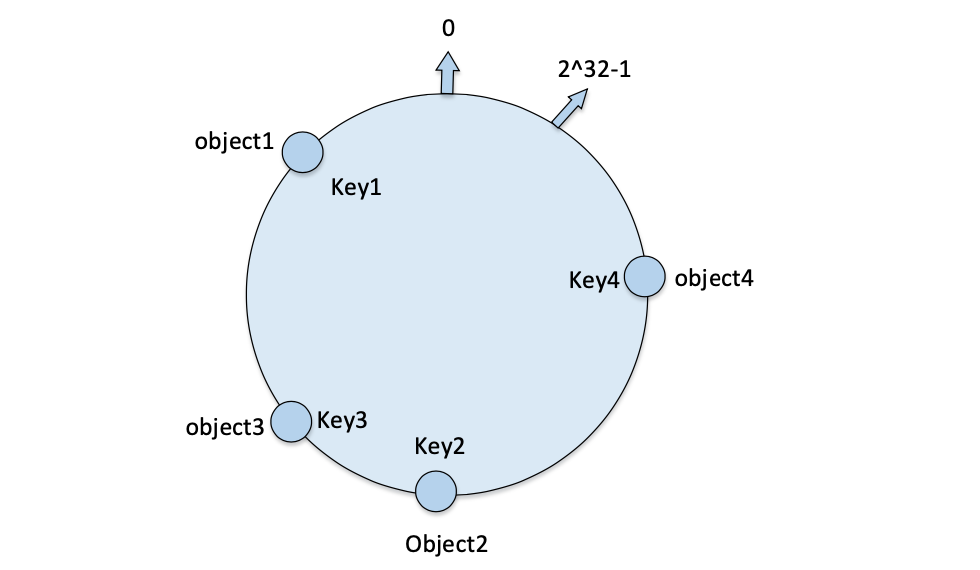

    1
2
3

    hash(object1) = key1;
......
hash(object4) = key4;

    Map numeric objects to a hash space

  3. Mapping machine nodes to a hash space: the same hash function is used for machine nodes to map to the ring address space. Consistent hashing uses the same hash function for numeric objects and machine nodes mapped into the same ring hash space. Then all data objects are stored to the nearest node along the ring address space in clockwise direction.

    Currently there exist node A , node B , node C a total of 3 machine nodes, through the calculation of the hash function, their mapping results on the ring address space will be shown in the figure, you can see that these machine nodes in the ring hash space, based on the corresponding hash value sorting.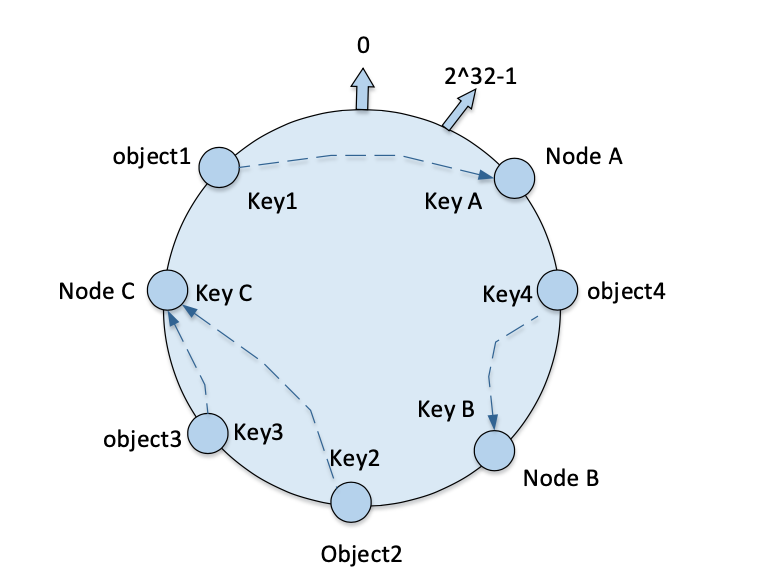

    1
2
3

    hash(node A) = key A;
......
hash(node C) = key C;

    Ring Hash Space

    Note: For the calculation of machine node hash values, the input to the hash function can be either the IP address of the machine or the string signature of the machine name.

    From the figure, we can see that all the numeric objects are in the same ring hash space with the machine nodes. The corresponding storage node is found clockwise from the location mapped to the numeric object, and the numeric object is stored to the first machine node found. Thus object1 is stored in node A, object3 is stored in node B, and object2 and object4 are both stored in node C. In such a clustered environment, the ring address space does not change, and by calculating the hash address space value of each numeric object, you can locate the corresponding machine node, that is, the machine where the numeric object is actually stored.

  4. Machine node addition and deletion: Consistent hashing can effectively avoid the cluster when a new node is added or deleted, all the numerical objects in the hash space of the entire system will change the address of the situation. For node changes only a small part of the data in the ring address space migration, avoiding the migration of a large amount of data, reducing the pressure on the server, with better fault tolerance and scalability.

    • Delete Machine

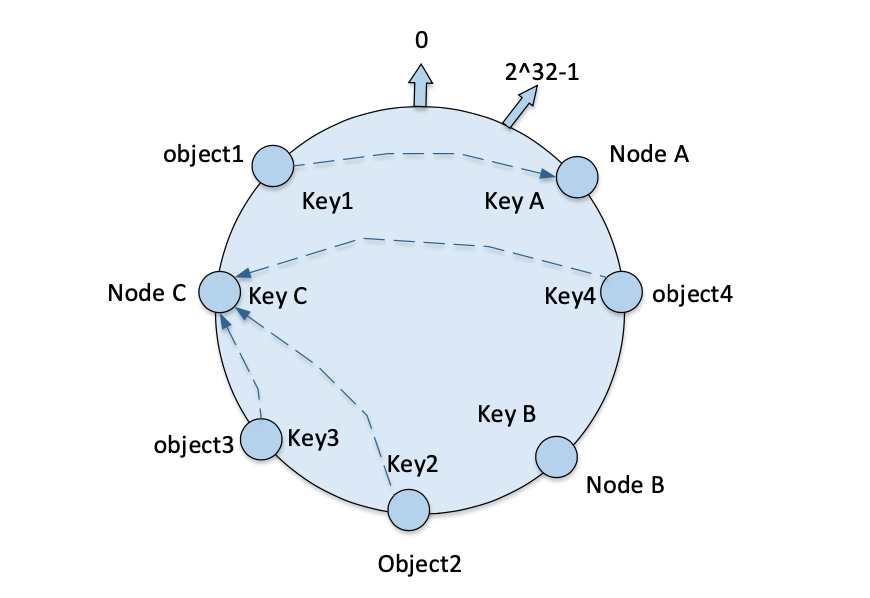
      Delete Machine

    • Adding machines

      Adding machines

Virtual Nodes

Consistent hashing algorithm corrects the defects of the simple hashing algorithm to ensure the monotonicity and dispersion of the hashing algorithm and load balancing requirements, but also needs to solve the problem of balance. By balanced, it means to try to distribute the hash result of numerical objects to all address spaces, which can make all address spaces are fully utilized and ensure the balance of system pressure load.

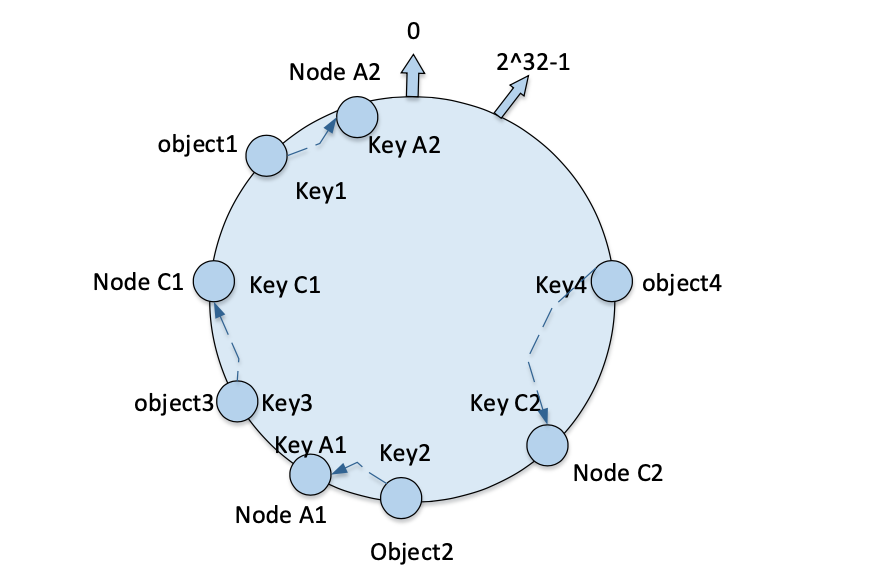
Consistent hashing algorithms are random in nature and do not strictly guarantee balance, for example, when the number of machines is small, numerical objects cannot be mapped evenly to all machines, in the above example, if only node A and node C are deployed, then node A stores only object1 while node C stores both object2, object3 and object4, such a mapping does not satisfy the balance requirement.

The introduction of virtual nodes can be a good solution to the problem of consistency hashing algorithm balance.

Virtual node is a copy of the actual machine node in the ring hash space, an actual machine node corresponds to multiple “virtual nodes”, “virtual nodes” in the ring hash space in hash value arrangement.

Without virtual nodes, only two machines node A and node C are deployed, as shown in the figure, the distribution of numerical objects on the machine nodes is very unbalanced. For this reason, virtual nodes are introduced and one actual physical node is set to correspond to two virtual nodes, so that there will be four “virtual nodes”, virtual nodes node A1 , node A2 correspond to actual physical node node A , virtual nodes node C1 , node C2 correspond to actual physical node node C, so that the distribution of numerical objects on each node is shown in the figure.

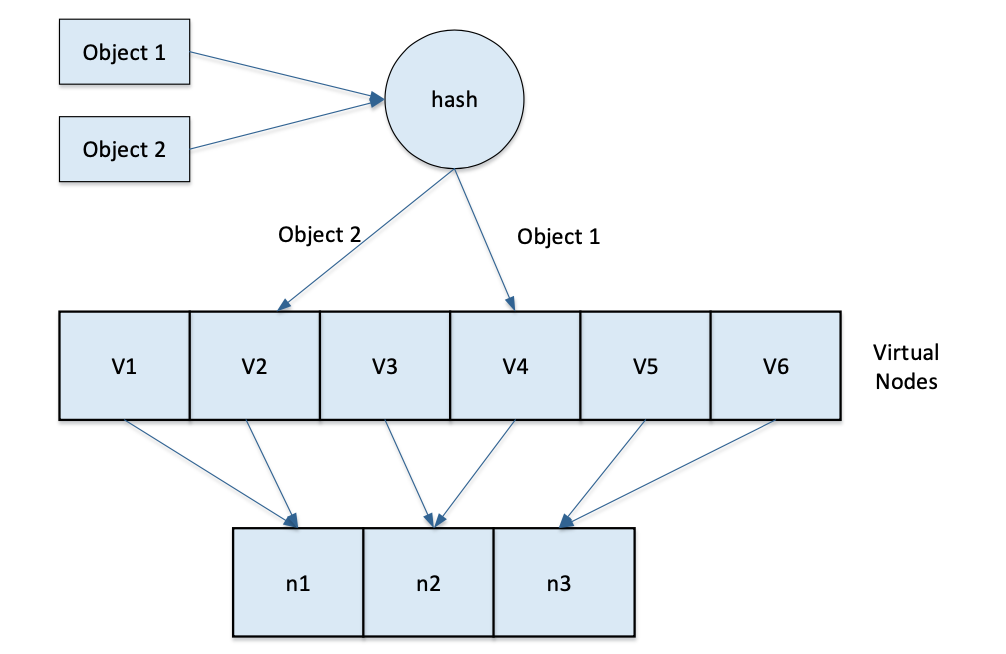
Virtual Nodes

In this case, the mapping of objects to “virtual nodes” is as follows.

1
2
3
4

objec1->node A2;
objec2->node A1;
objec3->node C1;
objec4->node C2;

Thus objects object1 and object2 are mapped to node A, while object3 and object4 are mapped to node C; the balance has been greatly improved.

With the introduction of virtual nodes, the previous mapping of numeric objects to machine nodes has changed from { numeric objects -> machine nodes } to { numeric objects -> virtual nodes -> actual physical nodes }. The mapping relationship when querying the node where the numeric object is located in this way is shown in the figure.

Virtual Nodes

The hash value of a “virtual node” is generally calculated by taking the IP address of the actual physical node plus a numeric suffix as input to the hash function. For example, suppose the IP address of node A is 202.168.14.241. Before the cluster is introduced to the “virtual node”, the hash of the actual physical machine node node A is calculated: Hash("202.168.14.241") After the cluster is introduced to the “virtual node After the “virtual nodes” are introduced to the cluster, the hashes of the “virtual nodes” node A1 and node A2 are computed.

1
2

Hash("202.168.14.241#1"); // cache A1
Hash("202.168.14.241#2"); // cache A2

Summary

In general, distributed systems require hashing to distribute load evenly, however simple hashing is not enough to solve the problem of minimizing the impact when a distributed cluster changes, so consistent hashing is needed to ensure that the hash ring changes and the cluster only requires a minimal amount of work to adapt. In addition, nodes need to exist in multiple locations on the ring to ensure that the load is statistically more likely to be distributed more evenly. Finally, “virtual nodes” need to be introduced to solve the balancing problem, ensuring that the hash results are distributed across all address spaces, so that all address spaces are fully utilized and the system pressure load is balanced.