Golang implementation of cuckoo filters

Introduction

In our work, if we encounter such things as web URL de-duplication, spam identification, or the determination of duplicate elements in a large collection, we usually think of saving all the elements in the collection and then determining them by comparison. If we use the best performance Hash table to make the determination, then as the number of elements in the collection increases, the storage space we need will also grow linearly and eventually reach the bottleneck.

So many times the choice is made to use a Bloom filter to do this. Bloom filters reduce the space cost significantly by mapping the keys stored in the bitmap to a fixed size binary vector or bitmap, and then to a mapping function. The complexity of the Bloom filter in terms of storage space and insertion/query time is a constant O(K). However, as the number of elements deposited increases, the Bloom filter miscalculation rate increases, and elements cannot be deleted.

Those who want to experience the insertion step of the Bloom filter can look here: https://www.jasondavies.com/bloomfilter/

So the Cuckoo filter was born. The disadvantages of the Bloom filter are stated directly in the paper Cuckoo Filter: Practically Better Than Bloom.

A limitation of standard Bloom filters is that one cannot remove existing items without rebuilding the entire filter.

The paper also mentions 4 major advantages of the cuckoo filter.

1. It supports adding and removing items dynamically;
2. It provides higher lookup performance than traditional Bloom filters, even when close to full (e.g., 95% space utilized);
3. It is easier to implement than alternatives such as the quotient filter; and
4. It uses less space than Bloom filters in many practical applications, if the target false positive rate is less than 3%.

Principle of implementation

Simple working principle

You can simply put the cuckoo filter inside two hash tables T1, T2, two hash tables corresponding to two hash functions H1, H2.

The specific insertion steps are as follows.

1. when a non-existent element is inserted, its position in the T1 table is first calculated according to H1, if the position is empty then it can be put in.
2. if the position is not empty, the position in the T2 table is calculated from H2 and can be put in if the position is empty. 3. if the T1 table and the T2 table are not empty, the position in the T2 table is calculated from H2 and can be put in if the position is empty.
3. if neither the T1 table nor the T2 table is empty, then a random hash table is selected to kick out the element.
4. the kicked element will cycle through to find its other position, and if it is temporarily kicked out, one will be randomly selected and the kicked element will cycle through to find its position again.
5. if there is a cycle of kicking out resulting in no elements being placed, then a threshold is set, beyond which the hash table is considered almost full, and it is then necessary to expand it and reposition all the elements.

An example is given below to illustrate this.

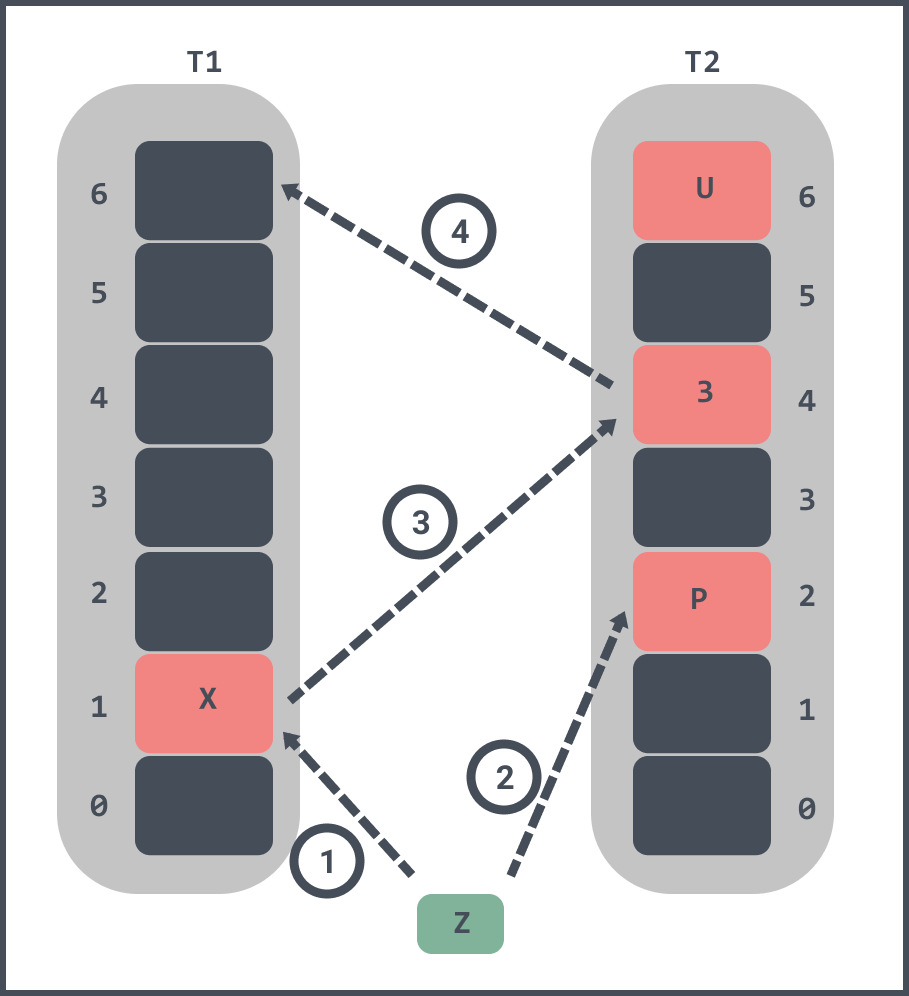
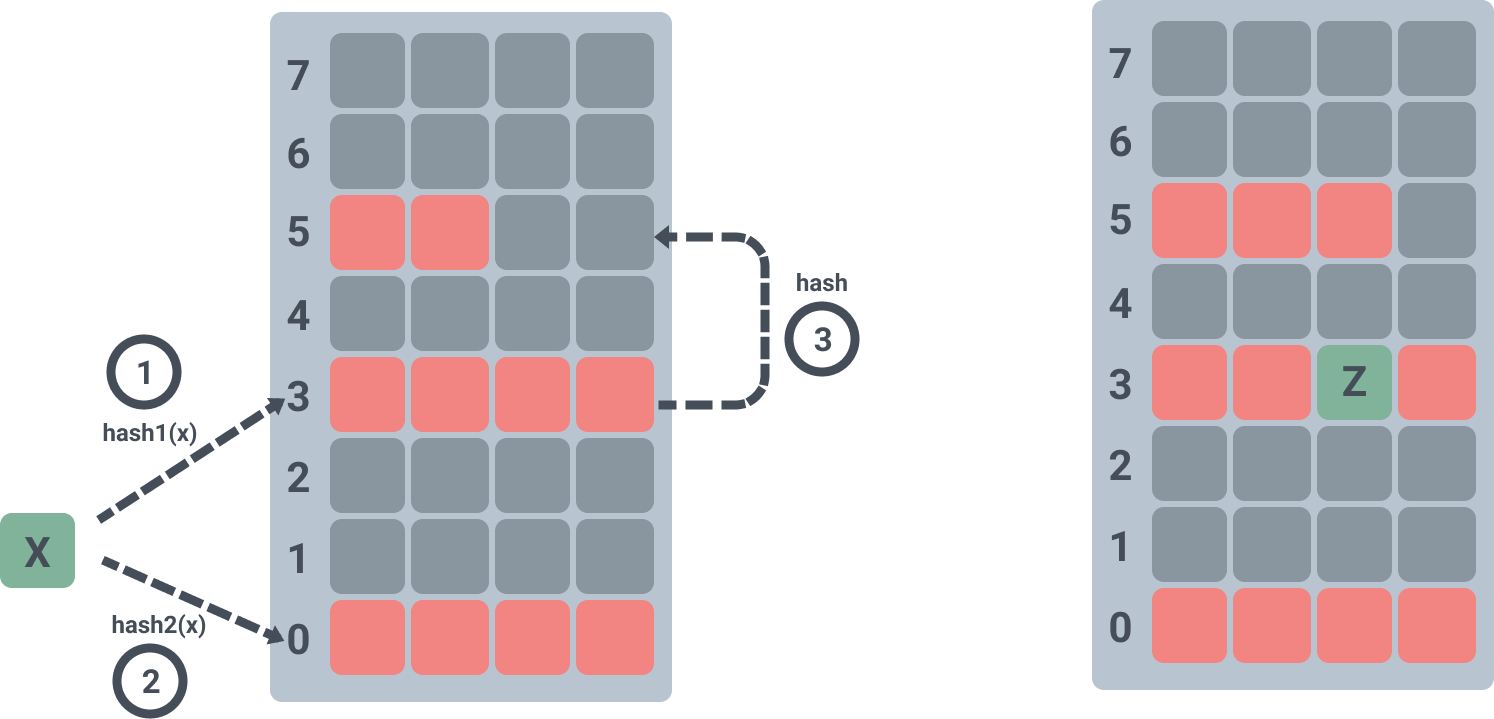
If you want to insert an element Z into the filter.

1. first Z will be hash-calculated and it is found that both slot 1 and slot 2 corresponding to T1 and T2 are already occupied.
2. randomly kicks out element X from slot 1 in T1, and slot 4 corresponding to T2 of X is already occupied by element 3.
3. kick out element 3 from slot 4 in T2, and element 3 is found to be empty in slot 6 of T1 after hash calculation, so element 3 is inserted into slot 6 of T1.

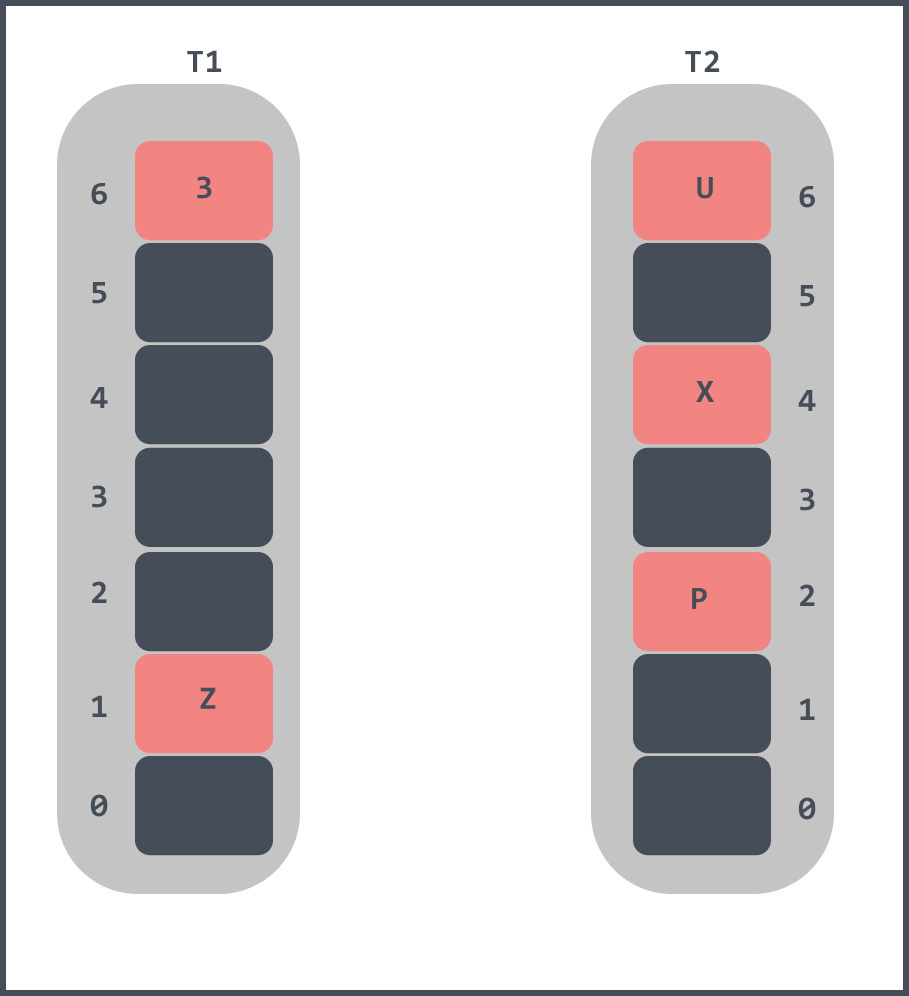
When Z has been inserted it looks like this.

Cuckoo filters

The cuckoo filter is similar in structure to the above implementation, except that the above array structure stores the entire element, whereas the cuckoo filter only stores a few bits of the element, called fingerprint information. Here, data accuracy is sacrificed in favour of space efficiency.

In the above implementation, each slot in the hash table can only hold one element, which is only 50% space efficient, whereas in the cuckoo filter each slot can hold multiple elements, turning it from one-dimensional to two-dimensional. The paper indicates that.

With k = 2 hash functions, the load factor α is 50% when the bucket size b = 1 (i.e., the hash table is directly mapped), but increases to 84%, 95% or 98% respectively using bucket size b = 2, 4 or 8.

The diagram below represents a two-dimensional array that can hold 4 elements per slot, and differs from the above implementation in that instead of using two arrays to hold them, only one is used.

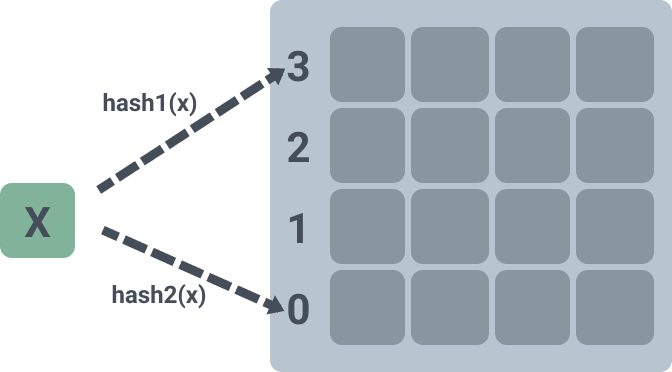
Having said that, here are the changes to the data structure, and here are the changes to the position calculation.

Our simple implementation of the position calculation formula above is done like this:

1
2

p1 = hash1(x) % arr length
p2 = hash2(x) % arr length

And the formula for calculating the position of the cuckoo filter can be seen in the paper as follows:

1
2
3
4
5

f = fingerprint(x);

i1 = hash(x);

i2 = i1 ⊕ hash( f);

We can see that the position i2 is calculated by taking an anomaly between i1 and the fingerprint information corresponding to the element X. The fingerprint information, as explained above, is a few bits of the element X, sacrificing some precision in exchange for space.

So why do we need to use an iso-or here? Because it is possible to use the self-reflexive nature of the iso-or: A ⊕ B ⊕ B = A, so that instead of knowing whether the current position is i1 or i2, the current position can be iso-ored with hash(f) to obtain another position.

One detail to note here is that the computation of i2 requires the hash of the fingerprint of element X before taking the iso-or, as the paper also shows.

If the alternate location were calculated by “i⊕fingerprint” without hashing the fingerprint, the items kicked out from nearby buckets would land close to each other in the table, if the size of the fingerprint is small compared to the table size.

If you do a direct diff, it is likely that i1 and i2 will be located very close to each other, especially in a small hash table, increasing the probability of collisions.

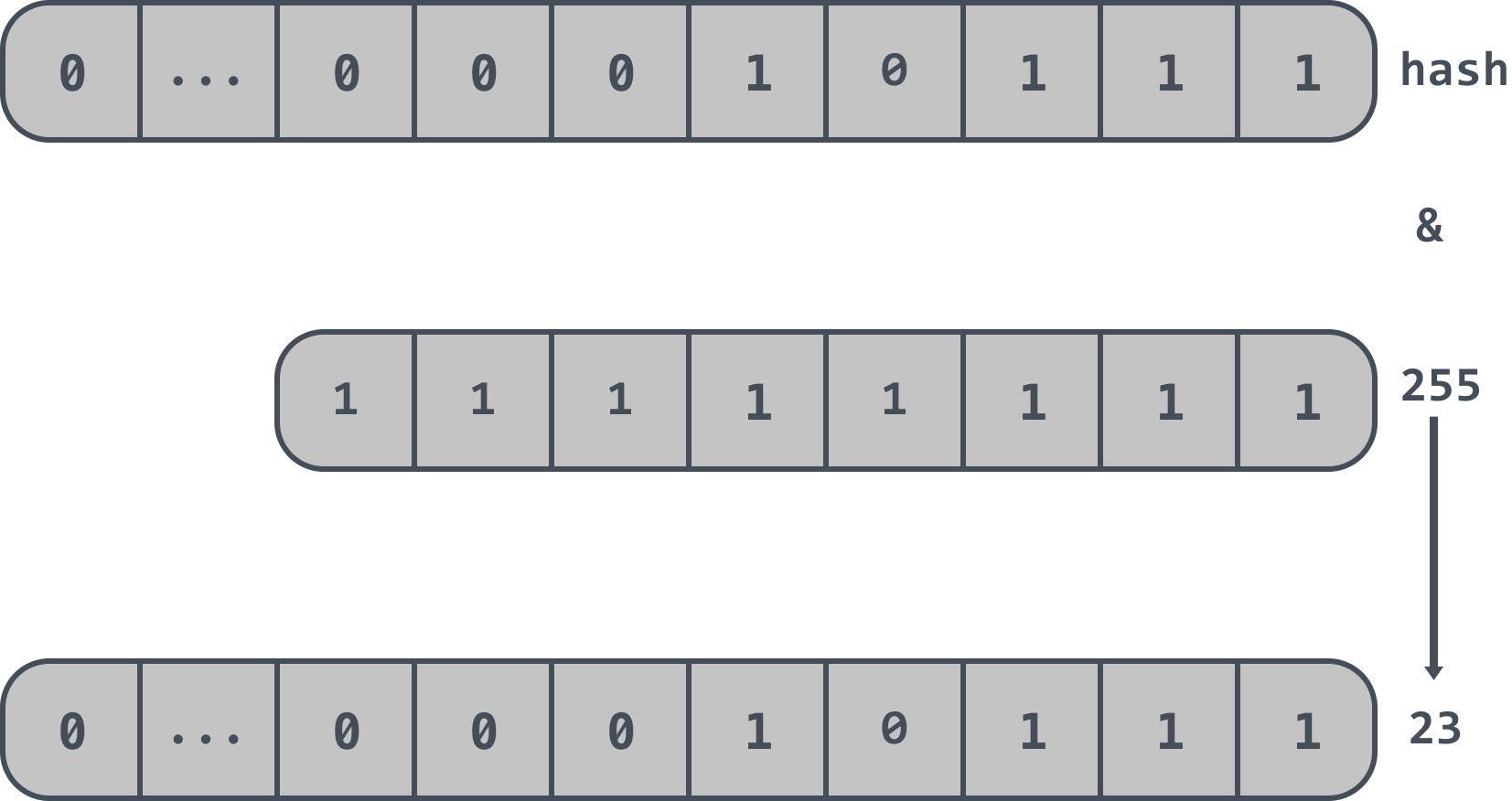
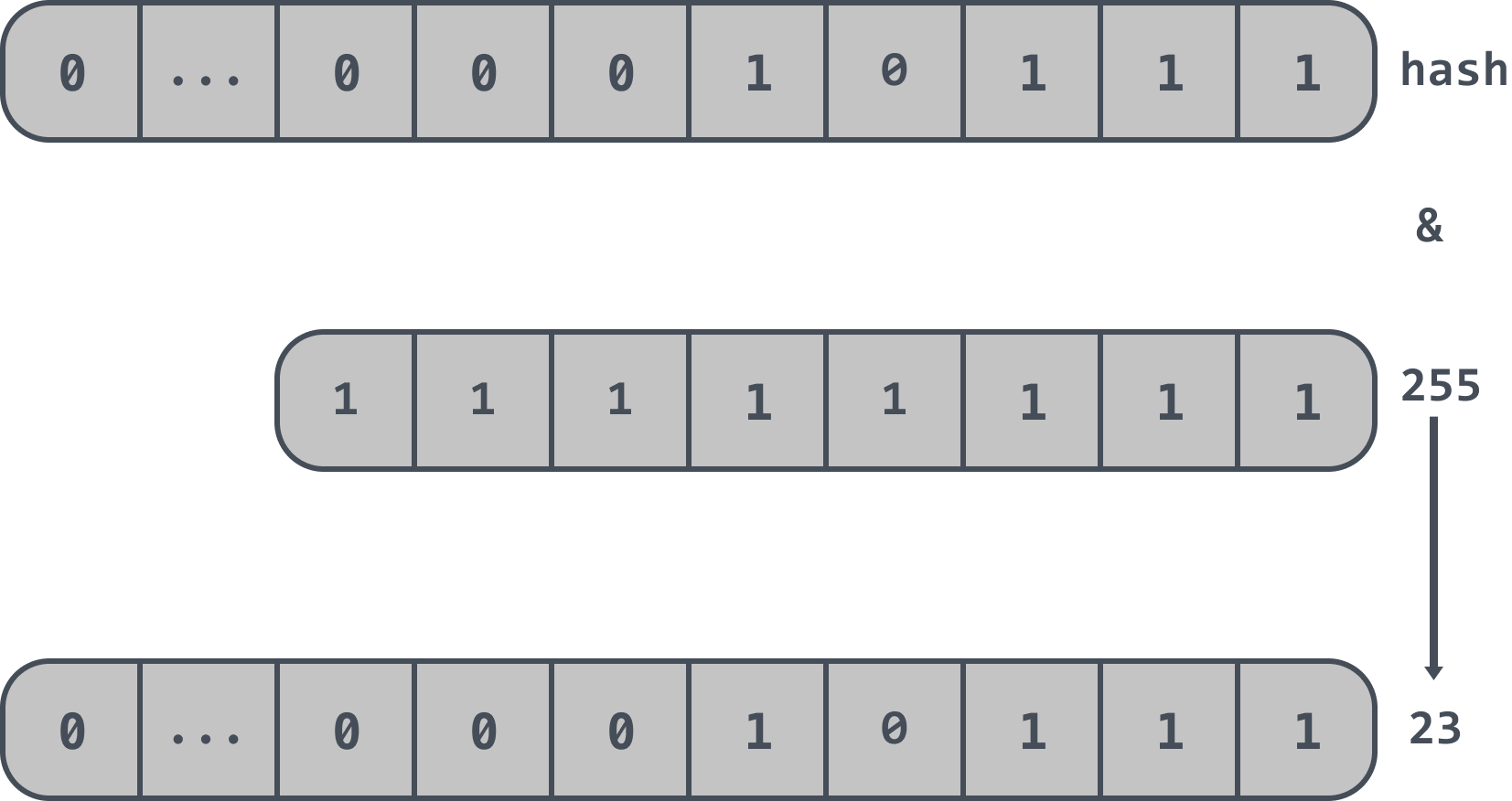
There is also a constraint that the cuckoo filter forces the length of the array to be an exponent of 2, so instead of modulo the length of the array, the cuckoo filter takes the last n bits of the hash value.

If the length of the array in a cuckoo filter is 2^8, i.e. 256, then the last n bits of the hash value are taken, i.e.: hash & 255, so that the final position information is obtained. The final position information is 23 as follows.

Code implementation

Data structure

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

const bucketSize = 4
type fingerprint byte
// 二维数组，大小是4
type bucket [bucketSize]fingerprint

type Filter struct {
    // 一维数组
    buckets   []bucket
    // Filter 中已插入的元素
    count     uint
    // 数组buckets长度中对应二进制包含0的个数
    bucketPow uint
}

Here we assume that a fingerprint fingerprint takes up 1byte of bytes and has 4 seats per location.

Initialisation

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

var (
    altHash = [256]uint{}
    masks   = [65]uint{}
)

func init() {
    for i := 0; i < 256; i++ {
        // 用于缓存 256 个fingerprint的hash信息
        altHash[i] = (uint(metro.Hash64([]byte{byte(i)}, 1337)))
    }
    for i := uint(0); i <= 64; i++ {
        // 取 hash 值的最后 n 位
        masks[i] = (1 << i) - 1
    }
}

The init function caches two global variables, altHash and masks. since the fingerprint length is 1byte, the initialization of altHash uses a 256 size array to cache the corresponding hash information to avoid having to recalculate it each time; masks is used to fetch the last n bits of the hash value. This will be used later.

We will use a NewFilter function to get the filter Filter by passing in the size of the filter that it can hold.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func NewFilter(capacity uint) *Filter {
    // 计算 buckets 数组大小
    capacity = getNextPow2(uint64(capacity)) / bucketSize
    if capacity == 0 {
        capacity = 1
    }
    buckets := make([]bucket, capacity)
    return &Filter{
        buckets:   buckets,
        count:     0,
        // 获取 buckets 数组大小的二进制中以 0 结尾的个数
        bucketPow: uint(bits.TrailingZeros(capacity)),
    }
}

The NewFilter function adjusts the capacity to an exponential multiple of 2 by calling getNextPow2, which returns 16 if the capacity passed in is 9; it then calculates the length of the buckets array and instantiates Filter; bucketPow returns the number of bits in the binary ending in 0. Since capacity is an exponential multiple of 2, bucketPow is the number of bits in the capacity binary minus 1.

Inserting elements

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

func (cf *Filter) Insert(data []byte) bool {
    // 获取 data 的 fingerprint 以及 位置 i1
    i1, fp := getIndexAndFingerprint(data, cf.bucketPow)
    // 将 fingerprint 插入到 Filter 的 buckets 数组中
    if cf.insert(fp, i1) {
        return true
    }
    // 获取位置 i2
    i2 := getAltIndex(fp, i1, cf.bucketPow)
    // 将 fingerprint 插入到 Filter 的 buckets 数组中
    if cf.insert(fp, i2) {
        return true
    }
    // 插入失败，那么进行循环插入踢出元素
    return cf.reinsert(fp, randi(i1, i2))
}

func (cf *Filter) insert(fp fingerprint, i uint) bool {
    // 获取 buckets 中的槽位进行插入
    if cf.buckets[i].insert(fp) {
        // Filter 中元素个数+1
        cf.count++
        return true
    }
    return false
}

func (b *bucket) insert(fp fingerprint) bool {
    // 遍历槽位的 4 个元素，如果为空则插入
    for i, tfp := range b {
        if tfp == nullFp {
            b[i] = fp
            return true
        }
    }
    return false
}

1. the getIndexAndFingerprint function will get the fingerprint of the data, and the position i1;
2. then call insert to insert into Filter’s buckets array, if the buckets array is full of 4 elements corresponding to slot i1, then try to get position i2 and try to insert the element into the corresponding slot i2 in the buckets array.
3. the corresponding slot i2 is also full, then call the reinsert method to randomly get a position in slots i1 and i2 to grab, then kick out the old element and repeat the insertion cycle.

Here’s how getIndexAndFingerprint gets the fingerprint and slot i1.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func getIndexAndFingerprint(data []byte, bucketPow uint) (uint, fingerprint) {
    // 将 data 进行hash
    hash := metro.Hash64(data, 1337)
    // 取 hash 的指纹信息
    fp := getFingerprint(hash)
    // 取 hash 高32位，对 hash 的高32位进行取与获取槽位 i1
    i1 := uint(hash>>32) & masks[bucketPow]
    return i1, fingerprint(fp)
}
// 取 hash 的指纹信息
func getFingerprint(hash uint64) byte {
    fp := byte(hash%255 + 1)
    return fp
}

After hashing the data in getIndexAndFingerprint, the result is modulo the fingerprint information, and then the higher 32 bits of the hash value are summed to get the slot i1. masks has already been seen during initialization, masks[bucketPow] gets the binary result of 1, which is used to get the lower bit of the hash. hash’s lower value.

If the initialization passes in a capacity of 1024, then the bucketPow is calculated to be 8, which gives masks[8] = (1 << 8) - 1, which is 255, the binary is 1111, 1111, and the high 32 of hash is summed to get the slot i1 in the final buckets.

1
2
3
4
5

func getAltIndex(fp fingerprint, i uint, bucketPow uint) uint {
    mask := masks[bucketPow]
    hash := altHash[fp] & mask
    return i ^ hash
}

The slot in getAltIndex is obtained by using altHash to obtain the hash value of the fingerprint information and then taking an iso-or to return the slot value. Note that due to the nature of the iso-or, either slot i1 or slot i2 can be passed in to return the corresponding other slot.

Here is a look at the loop kick out insert reinsert.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

const maxCuckooCount = 500

func (cf *Filter) reinsert(fp fingerprint, i uint) bool {
    // 默认循环 500 次
    for k := 0; k < maxCuckooCount; k++ {
        // 随机从槽位中选取一个元素
        j := rand.Intn(bucketSize)
        oldfp := fp
        // 获取槽位中的值 
        fp = cf.buckets[i][j]
        // 将当前循环的值插入
        cf.buckets[i][j] = oldfp

        // 获取另一个槽位
        i = getAltIndex(fp, i, cf.bucketPow)
        if cf.insert(fp, i) {
            return true
        }
    }
    return false
}

This will loop through the slots a maximum of 500 times to get the slot information. Since each slot can hold up to 4 elements, rand is used to randomly kick out an element from one of the 4 slots, insert the element from the current loop, get the information of the other slot of the kicked out element, and call insert again.

The above diagram shows that when element X is inserted into the hash table, it is hashed twice to find that the corresponding slots 0 and 3 are full, so one of the elements in slot 3 is randomly seized and the seized element is re-hashed and inserted into the third position of slot 5.

Querying data

When you query the data, you are looking to see if there is a corresponding fingerprint in the corresponding position.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

func (cf *Filter) Lookup(data []byte) bool {
    // 获取槽位 i1 以及指纹信息
    i1, fp := getIndexAndFingerprint(data, cf.bucketPow)
    // 遍历槽位中 4 个位置，查看有没有相同元素
    if cf.buckets[i1].getFingerprintIndex(fp) > -1 {
        return true
    }
    // 获取另一个槽位 i2
    i2 := getAltIndex(fp, i1, cf.bucketPow)
    // 遍历槽位 i2 中 4 个位置，查看有没有相同元素
    return cf.buckets[i2].getFingerprintIndex(fp) > -1
}

func (b *bucket) getFingerprintIndex(fp fingerprint) int {
    for i, tfp := range b {
        if tfp == fp {
            return i
        }
    }
    return -1
}

Deleting data

When you delete data, you also just erase the fingerprint information on that slot.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

func (cf *Filter) Delete(data []byte) bool {
    // 获取槽位 i1 以及指纹信息
    i1, fp := getIndexAndFingerprint(data, cf.bucketPow)
    // 尝试删除指纹信息
    if cf.delete(fp, i1) {
        return true
    }
    // 获取槽位 i2
    i2 := getAltIndex(fp, i1, cf.bucketPow)
    // 尝试删除指纹信息
    return cf.delete(fp, i2)
}

func (cf *Filter) delete(fp fingerprint, i uint) bool {
    // 遍历槽位 4个元素，尝试删除指纹信息
    if cf.buckets[i].delete(fp) {
        if cf.count > 0 {
            cf.count--
        }
        return true
    }
    return false
}

func (b *bucket) delete(fp fingerprint) bool {
    for i, tfp := range b {
        // 指纹信息相同，将此槽位置空
        if tfp == fp {
            b[i] = nullFp
            return true
        }
    }
    return false
}

Disadvantages

After implementing the cuckoo filter, let’s think about what would happen if the cuckoo filter did multiple consecutive insertions of the same element.

Then the element would hog all the positions on both slots and eventually, when the 9th identical element was inserted, it would keep cycling and squeezing until the maximum number of cycles, and then return a false.

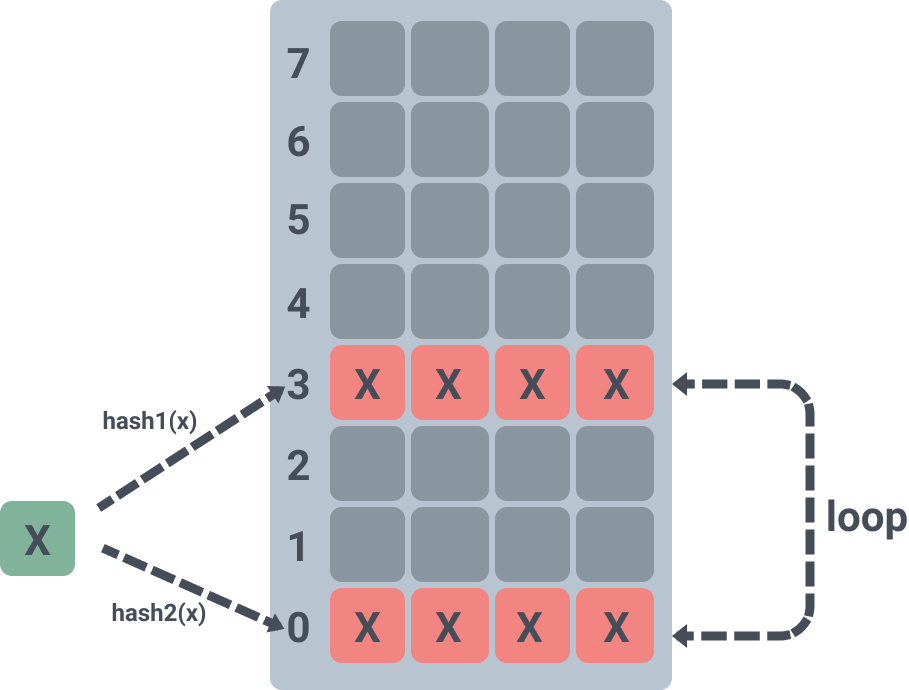
Would it solve the problem if a check was done before insertion? This would indeed not result in a circular squeeze, but there would be a certain probability of a false positive situation.

As we can see from the above implementation, the fingerprint information set in each location is 1byte and there are 256 possibilities. If two elements have the same hash location and the same fingerprint, then this insertion check will assume that they are equal leading to the assumption that the element already exists.

In fact, we can reduce the probability of false positives by adjusting the amount of fingerprint information stored, e.g. in the above implementation the probability of false positives is 0.03 for a 1byte fingerprint with 8 bits of information, when the fingerprint information is increased to 2bytes with 16 bits of information the probability of false positives is reduced to 0.0001.